ریاضیات روش هایی دارد که باعث می شود روی یک بیش از یک بار فکر کنیم و همه مسیر را دوباره انجام دهیم. ریاضیات با وجود فرم ها، عملیات و مشتقات آن به اندازه کافی گیج کننده است، با این حال افراد ممکن با تعاریف و اصطلاحات مشابه نیز گیج شوند. اغلب ما می دانیم که هندسه، علم محاسبات اندازه زمین، فضا و شکل ها است و وقتی کسی به هندسه فکر می کند، به احتمال اصطلاح "مساحت" به ذهن او خطور کند.
مساحت اشکال، فضایی است که با مرز محیط اشکال هندسی داده شده احاطه یا محصور شده است. اشکال دوبعدی اشکالی هستند که به راحتی می توان بر روی صفحه ترسیم کرد مانند مربع، مستطیل، مثلث، متوازی الاضلاع، ذوزنقه و غیره و محیط محصور شده اطراف آنها را به عنوان مساحت محاسبه کرد. در این مقاله سلام دنیا مساحت اشکال هندسی، فرمول های مساحت اشکال مختلف، مساحت اشکال دو بعدی، مساحت اشکال سه بعدی و غیره را مطالعه خواهید کرد.
مساحت چیست؟
مساحت به طور متداول، یک عبارت برای بیان اندازه یک سطح دو بعدی است و در واحدهای مختلف بیان می شود. از جمله: متر مربع، هکتار، کیلومتر مربع، فوت مربع، یارد مربع، مایل مربع و موارد دیگر.
تفاوت بین "مساحت" و "مساحت کل"
مساحت اغلب با "مساحت کل" اشتباه گرفته می شود، که اگر سطح دو بعدی باشد از نظر فنی یکسان است. با این حال، برای بیان مساحت یه جسم جامد و سه بعدی، استفاده از فرمول های مساحت کل مناسب تر است. برای مثال، یک مکعب دارای شش وجه با اندازه های یکسان است و مساحت کل آن برابر با مجموع مساحت های همه شش وجه آن خواهد بود (6s²).
فرمول مساحت کل
فرمول مساحت سطح یک راه حل ریاضی برای یافتن مساحت کل هر جسم سه بعدی است که توسط تمام سطوح آن اشغال شده است. اجازه دهید در ادامه با جزئیات در مورد فرمول های مساحت سطح اشکال مختلف سه بعدی آشنا شویم.
حتما بخوانید: فرمول محیط مربع چیست با مثال برای پایه سوم تا ششم
فرمول مساحت سطح چیست؟
فرمول مساحت سطح برای یافتن مجموع تمام مساحت های هر جسم سه بعدی استفاده می شود. فرمول سطح به دو دسته طبقه بندی می شود:
- فرمول مساحت سطح منحنی یا فرمول مساحت سطح جانبی
- فرمول مساحت سطح کل
به نمودار فرمول های مساحت سطح زیر نگاه کنید که فرمول های سطح شکل های سه بعدی مربوطه را نشان می دهد.
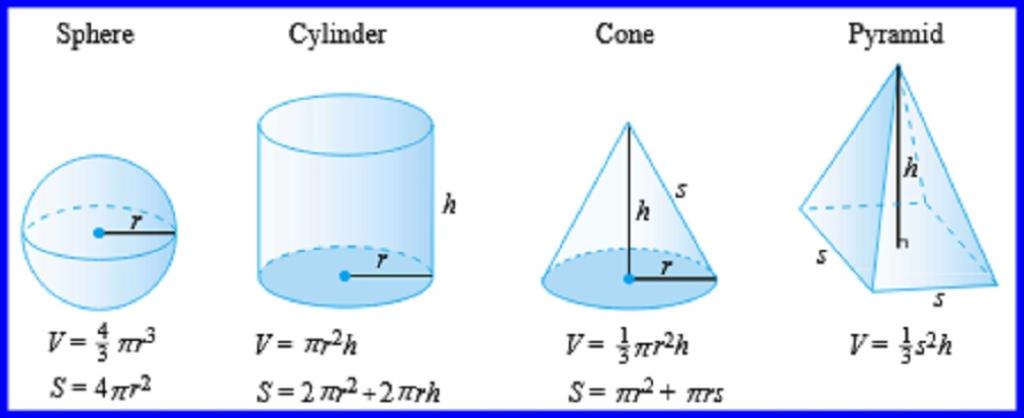
فرمول های مساحت اشکال هندسی مختلف
هر جسم سه بعدی دارای سطوح جانبی و سطح پایه است. مساحت سطح کل به مجموع مساحت سطح جانبی/منحنی و سطح پایه اشاره دارد. در این بخش با فرمول های مساحت اشکال مختلف سه بعدی آشنا می شویم.
فرمول مساحت سطح مکعب
مساحت سطح مکعب کل مساحتی است که هر شش وجه مکعب پوشانده اند. فرمول کلی سطح یک مکعب به صورت زیر است:
- فرمول سطح کل مکعب، مجموع مساحت سطوح عمودی مکعب و مساحت پایه خواهد بود. فرمول سطح کل مکعب = 6a2 که در آن "a" طول ضلع است.
- فرمول سطح جانبی یک مکعب مجموع مساحت تمام وجوه جانبی مکعب است. LSA = 4a2 که در آن "a" طول ضلع است.
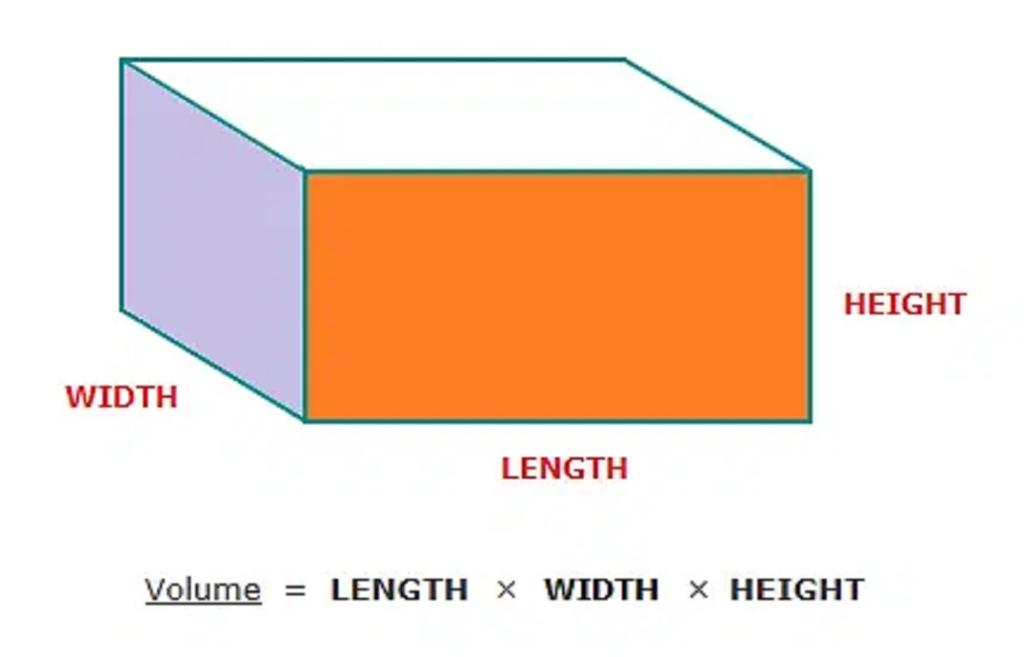
فرمول مساحت مکعب مستطیل
فرمول مساحت کل مکعب مستطیل با جمع مساحت هر 6 وجه به دست می آید. سطح کل و سطح جانبی را می توان بر حسب ابعاد آن بیان کرد: طول (l)، عرض (b) و ارتفاع مکعب (h) به صورت:
- سطح کل مکعب، S = 2 (lb + bh + lh) واحد2
- مساحت سطح جانبی مکعب، L = 2h (l + b) واحد2
فرمول مساحت مخروط
مخروط یک شکل سه بعدی است که دارای پایه دایره ای با شعاع "r" و قطر "d" است. این شکل یک مساحت سطح منحنی دارد، بنابراین می توانیم فرمول مساحت سطح منحنی آن و همچنین فرمول مساحت کل را داشته باشیم. اگر شعاع قاعده مخروط "r" و ارتفاع شیب مخروط "l" باشد، سطح مخروط به صورت زیر در نظر گرفته می شود:
- سطح کل مخروط، T = πr(r + l)
- سطح منحنی یک مخروط، S = πrl
فرمول مساحت استوانه
یک استوانه دارای یک سطح منحنی است که دو پایه دایره ای در دو انتها قرار گرفته است. اگر شعاع قاعده استوانه "r" و ارتفاع استوانه "h" باشد، مساحت استوانه به صورت زیر در نظر گرفته می شود:
- مساحت کل استوانه ، T = 2πr(h + r)
- مساحت سطح منحنی یک استوانه، S = 2πrh
حتما بخوانید: روش محاسبه مساحت مربع با مثال برای همه پایه ها
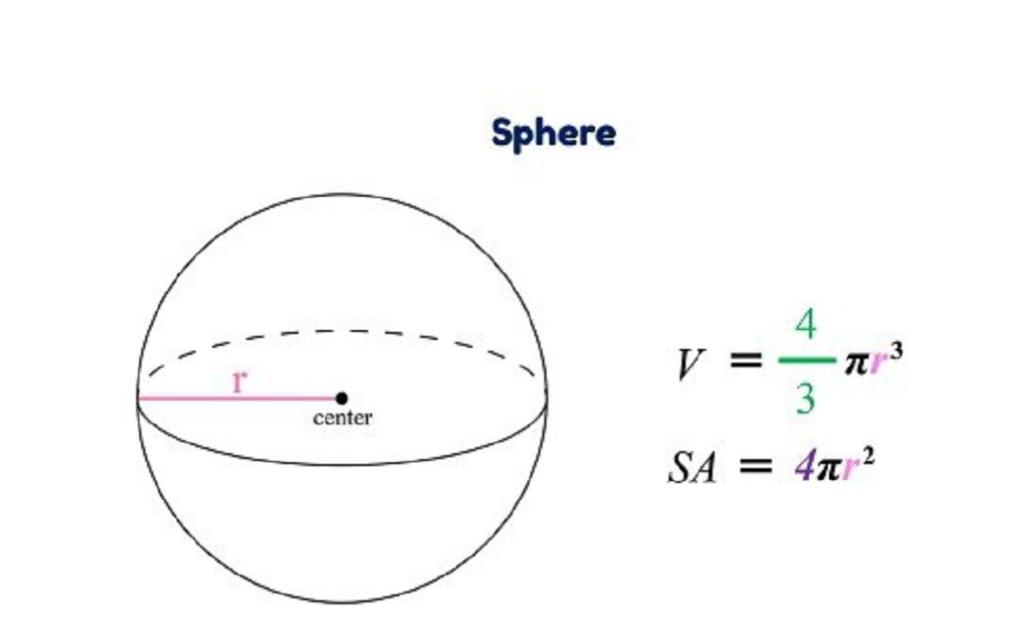
فرمول مساحت کره
کره یک جسم جامد سه بعدی با ساختاری گرد است. مساحت یک کره، مساحت کل وجوه اطراف آن است. فرمول مساحت کره به صورت زیر است:
مساحت کره، S = 4πr2 واحد مربع ⇒
فرمول مساحت نیمکره
نیمکره نیمی از یک کره است. مساحت یک نیمکره کل مساحتی است که سطح آن را می پوشاند. فرمول مساحت نیمکره را می توان به دو دسته تقسیم کرد:
- مساحت سطح منحنی یک نیمکره (CSA) = ½ (مساحت سطح منحنی یک کره) = ½ (4 π r2) = 2 π r2، که در آن "r" شعاع نیمکره است.
- مساحت کل یک نیمکره (TSA) = سطح منحنی + مساحت پایه = 2 πr2 + π r2 = 3 π r2، که در آن "r" شعاع نیمکره است.
فرمول مساحت منشور
مساحت سطح جانبی یک منشور مجموع مساحت تمام وجوه جانبی آن است در حالی که مساحت کل یک منشور مجموع مساحت جانبی و مساحت پایه های آن است. فرمول های مساحت سطح منشور را می توان به صورت زیر ارائه داد.
- مساحت سطح جانبی منشور = محیط پایه × ارتفاع
- مساحت کل یک منشور = سطح جانبی منشور + مساحت دو پایه = (2 × مساحت پایه) + سطح جانبی یا (2 × مساحت پایه) + (محیط پایه × ارتفاع).
بر اساس شکل پایه منشورها هفت نوع منشور وجود دارد. پایه انواع مختلف منشورها متفاوت است، بنابراین فرمول های تعیین مساحت سطح منشور نیز متفاوت است.
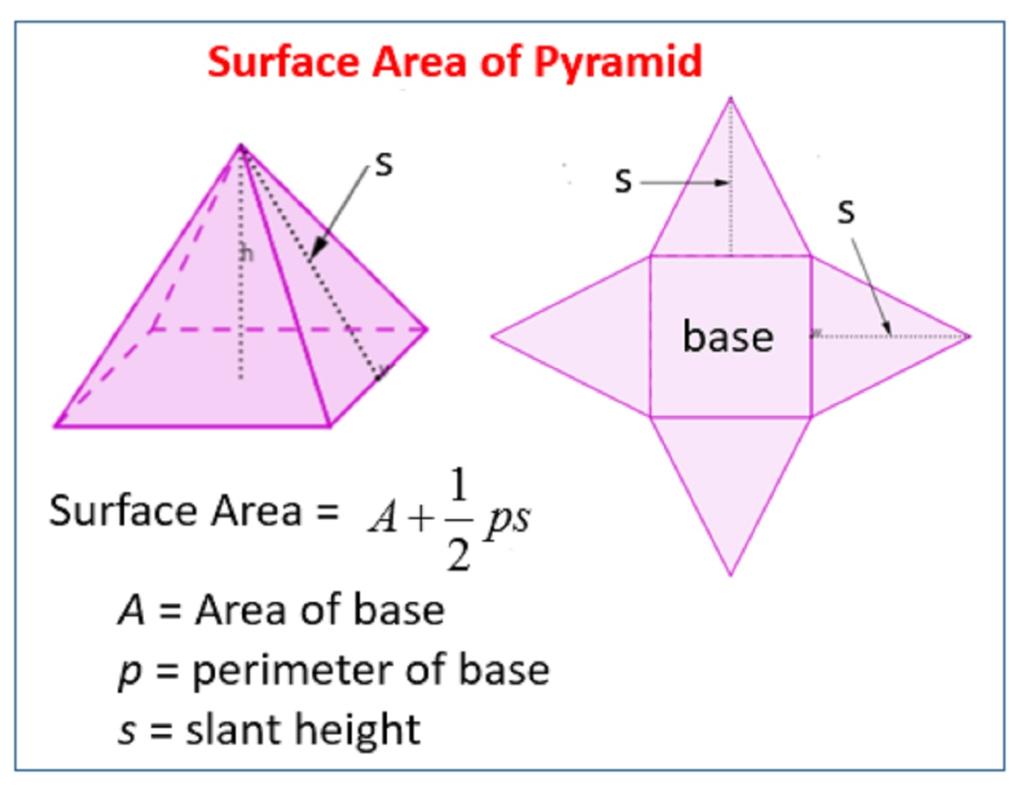
فرمول مساحت هرم
اگر یک هرم دارای یک قاعده چند ضلعی منظم با ارتفاعی باشد که از مرکز پایه عبور می کند، فرمول مساحت سطح جانبی و سطح کل برای هرم را می توان به صورت زیر ارائه کرد:
هرمی منظم را در نظر بگیرید که محیط قاعده آن 'P'، سطح پایه 'B'، و ارتفاع مایل (ارتفاع هر مثلث) 's' است.پس.
- مساحت سطح جانبی هرم (LSA) = (1/2) Ps
- مساحت کل هرم (TSA) = LSA + سطح پایه = (1/2) Ps + B
فرمول مساحت چند ضلعی
چند ضلعی یک شکل دو بعدی است که از خطوط مستقیم تشکیل شده است. چند نمونه از اشکال چند ضلعی عبارتند از مثلث، پنج ضلعی، شش ضلعی، مربع، مستطیل و غیره که نام این اشکال به خودی خود تعداد کل اضلاع موجود در شکل را مشخص می کند. به عنوان مثال، یک مثلث دارای 3 ضلع و یک مستطیل دارای 4 ضلع است. بنابراین، هر شکلی که از به هم پیوستن سه خط تشکیل شده باشد، به عنوان مثلث شناخته می شود، در حالی که اشکالی که از به هم پیوستن چهار خط ساخته شده اند، به عنوان چهار ضلعی شناخته می شوند. مساحت محدوده ای در داخل مرز/محیط است که باید بررسی شود.
حتما بخوانید: استفاده از ماشین حساب مهندسی کاسیو (Casio) با آموزش کامل تصویری
مساحت اشکال دو بعدی
در هندسه، اشکال دوبعدی به شکل صفحه یا شکل مسطحی که شامل دو معیار طول و عرض است، تعریف میشود. ضخامت در اشکال 2 بعدی وجود ندارد. مساحت و محیط دو معیار متفاوتی هستند که برای اندازه گیری اشکال مسطح استفاده می شوند. دو بعدی را می توان به راحتی روی یک کاغذ ساده ترسیم کرد. برخی از نمونه های اشکال دو بعدی مستطیل، مثلث، مربع، ذوزنقه و غیره هستند.
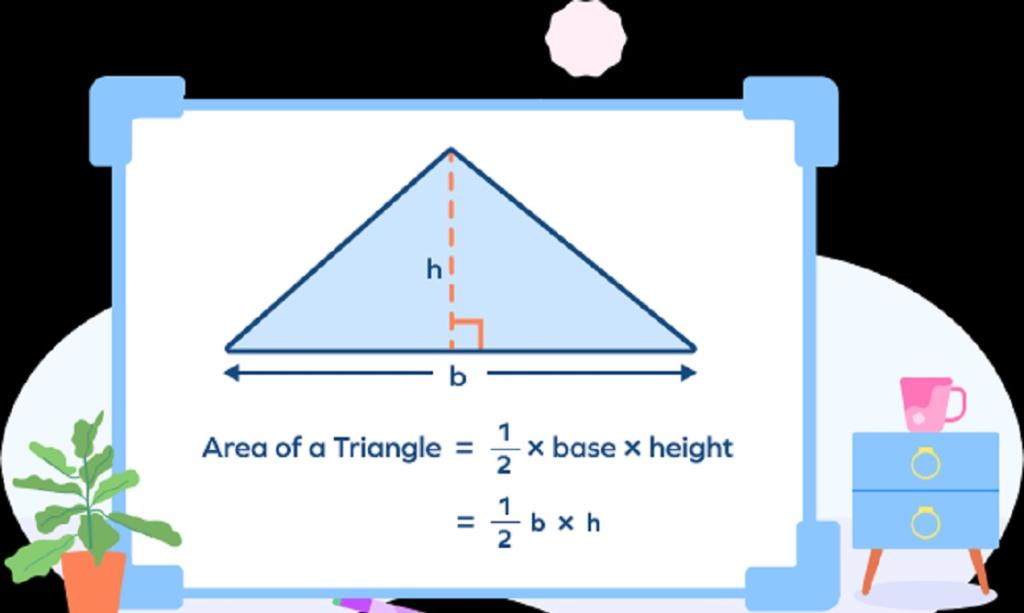
فرمول مساحت شکل های دو بعدی
به طور کلی، مساحت اشکال به عنوان مقدار رنگ مورد نیاز برای پوشش هر یک از سطوح با یک لایه تعریف می شود. در اینجا روش هایی برای محاسبه مساحت بر اساس اضلاع موجود در شکل به شرح زیر آمده است:
| شکل هندسی | فرمول مساحت |
| دایره | «شعاع × شعاع × عدد پی» یا πr2 |
| مثلث | 2 ÷ (قاعده × ارتفاع) |
| مستطیل | طول × عرض |
| متوازی الاضلاع | ارتفاع × قاعده |
| ذوزنقه | نصف ارتفاع × (قاعده بزرگ + قاعده کوچک) |
| بیضی | 14/3 × (نصف قطر کوچک × نصف قطر بزرگ) |
مثال هایی با استفاده از فرمول مساحت اشکال هندسی
1. مساحت سطح دایره ای که شعاع آن 7 سانتی متر است را محاسبه کنید.
شعاع سطح دایره ای = 7 سانتی متر (داده شده)،و همانطور که می دانیم مساحت دایره πr² است. بر این اساس:
فرمول مساحت = π × r × r
مساحت = 22/7 × 7 × 7
مساحت = 154 متر مربع
2. مساحت مخروطی که شعاع آن 4 سانتی متر و ارتفاع آن 3 سانتی متر است را محاسبه کنید.
شعاع یک مخروط = 4 سانتی متر و ارتفاع یک مخروط = 3 سانتی متر (Gven) و همانطور که گفته شد، فرمول مساحت مخروط πr(r + l) است.
ارتفاع مایل= l 4²+3²−−−−−−√
= 25−−√
سانتی متر 5 =
فرمول مساحت مخروط = πr(r + l)
A = 22/7 × 4 (4 + 5)
A = 22/7 × 4 (9)
A= 22/7 × 36
سانتی متر مربع A = 113.14
3. یک مخزن استوانه ای دارای شعاع 4 yd و ارتفاع 8 yd است که با استفاده از فرمول مساحت سطح استوانه مساحت سطح آن را پیدا کنید.
می دانیم که فرمول کل سطح استوانه = مساحت سطح منحنی استوانه + مساحت سطح بالا و پایین،بر اساس فرمول مساحت سطح استوانه:
=2πrh + 2πr2
=2πr(r + h)
301.68 =2 × 22/7 × 4 × (4 + 8)
4. با استفاده از فرمول سطح مکعب، سطح مکعبی را که ضلع آن 4 اینچ است را پیدا کنید.
با توجه به طول ضلع مکعب = 4 اینچ و فرمول سطح مکعب = 6a2 و اینکه a = 4 اینچ است مساحت مکعب به صورت زیر می باشد:
= 6 (4) 2
= 6 (16)
= 96 اینچ 2
فرمول های مساحت اشکال هندسی مختلف به طور خلاصه
یکی از اصلی ترین فرم های مساحت، مربوط به مستطیل است که طول آن در عرض (L × W) ضرب می شود، و در مورد مربع، طول ضلع آن به توان دو می رسد (s²).
سایر فرمول ها عبارتند از:
1. مساحت مثلث: (½ bh)؛ که b قاعده و h ارتفاع است.
2. مساحت لوزی: (½ ab)؛ که a و b دو قطر لوزی هستند.
3. مساحت متوازی الاضلاع: (bh)؛ که b طول قاعده و h ارتفاع عمود بر آن است.
4. مساحت ذوزنقه: (½ (a + b)h)؛ که a و b، طول دو ضلع موازی هم و h ارتفاع است.
5. مساحت دایره: (pr²)؛ که r طول شعاع دایره (مجدوز شعاع در عدد پی) است.
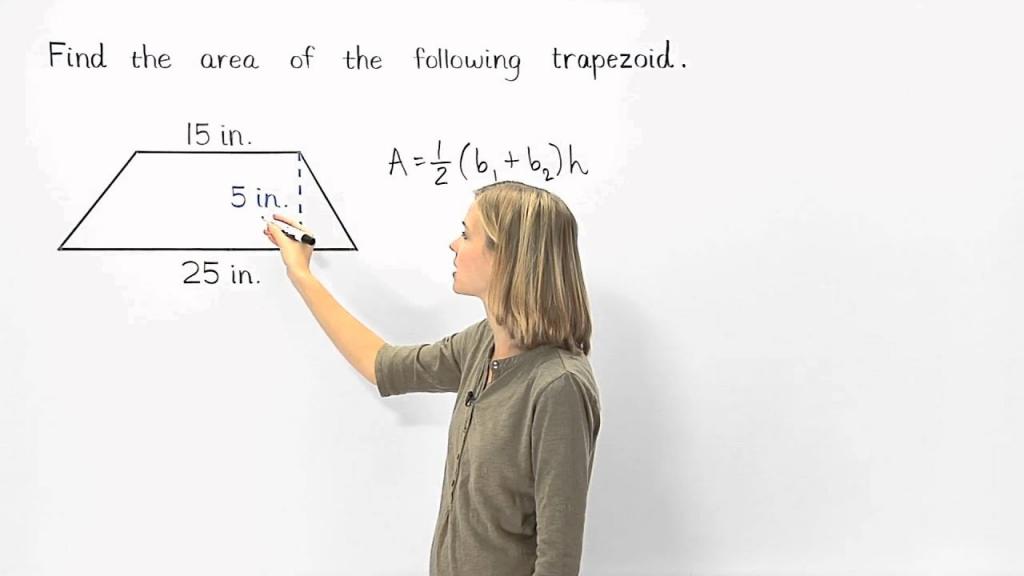
فرمول مساحت کل اشکال مختلف هندسی
مانند مساحت، مساحت کل در واحد مربع بیان می شود. فرمول مساحت کل برای برخی مواد جامد عبارتند از:
1. مساحت کل استوانه: ((2pr²(r + h)؛ که r شعاع، و h ارتفاع استوانه است.
2. مساحت کل مخروط: ((pr(r + l)؛ r شعاع و l ارتفاع شیب مخروط است.
3. مساحت کل کره: (4pr²)؛ که r شعاع است.
سوالات متداول:
1. فرمول مساحت سطح برای مکعب مستطیل چیست؟
فرمول سطح مکعب 2 (lb + bh + hl) است. در اینجا «l»، «b» و «h» سه بعد طول، عرض و ارتفاع مکعب را نشان میدهند.
2. رابطه بین فرمول مساحت سطح منحنی برای کره و نیمکره چیست؟
فرمول مساحت سطح منحنی یک نیمکره نصف مساحت سطح منحنی یک کره است. به صورت زیر آورده شده است:
CSA نیمکره = ½ (مساحت سطح منحنی یک کره) = ½ (4 π r2) = 2 π r2، که در آن "r" شعاع نیمکره/کره است.
3. فرمول مساحت سطح یک مخروط چیست؟
- فرمول مساحت کل یک مخروط به صورت T = πr(r + l) داده می شود.
- فرمول مساحت سطح منحنی یک مخروط به صورت S = πrl است.
- در اینجا "r" شعاع قاعده مخروط و "l" ارتفاع مایل مخروط است.
4. فرمول مساحت سطح استوانه چیست؟
فرمول مساحت یک استوانه، کل ناحیه پوشیده شده توسط سطح شکل استوانه ای است. از نظر ریاضی به صورت 2πr(h+r) بیان می شود، که در آن 'r' شعاع پایه دایره ای استوانه و 'h' ارتفاع استوانه است. مساحت سطح یک استوانه به واحدهای مربعی داده می شود، مانند m2، in2، cm2، yd2 و غیره.
نتیجه گیری
اصطلاح مساحت یک اصطلاح کلی برای بیان اندازه یک سطح است، در حالی که مساحت کل برای بیان اندازه سطح یک جسم جامد خاص استفاده می شود. مساحت برای سطوح مسطح دو بعدی کاربرد دارد، در حالی که مساحت کل برای اجسام جامد سه بعدی به کار می رود.
همانطور که با خواندن این مطلب متوجه شدید مساحت، اندازه درون شکلهای دوبعدی و سطح بیرونی شکلهای سهبعدی است.در این مطلب ما فرمول های "مساحت "و "مساحت کل" اشکال هندسی مختلف را در اختیار شما عزیزان قرار داده این تا بتوانید به راحتی مساحت اشکال هندسی مختلف را بدست بیاورید.
مطالب مرتبط:
روش محاسبه محیط و مساحت ذوزنقه تصویری و به زبان ساده با مثال
زنگ آهن چیست ؛ نام علمی و 4 راه جلوگیری از آن


دیدگاه ها