پیدا کردن زاویه سوم مثلث زمانی که اندازه گیری دو زاویه دیگر را می دانید عملی بسیار آسان می باشد. شما تنها کاری که باید انجام دهید این است که اندازه های دیگر زاویه را از 180 درجه کم کنید تا اندازه گیری زاویه سوم به دست آید. بسته به مشکلی که با آن مواجهه شدید، چند راه دیگر برای یافتن اندازه گیری زاویه سوم مثلث وجود دارد که در این مطلب به آن خواهیم پرداخت. در این مطلب سلام دنیا، ما به بدست آوردن ضلع سوم مثلث؛ پیدا کردن زاویه سوم مثلث؛ بدست آوردن زاویه مثلث با از روی اضلاع؛ محاسبه زاویه سوم مثلث متساوی الساقین، متساوی الاضلاع و قائم الزاویه به صورت تصویری و گام به گام پرداخته ایم. با ما همراه باشید.
نحوه پیدا کردن زاویه سوم مثلث
1. نحوه پیدا کردن زاویه سوم مثلث با استفاده از دو زاویه دیگر
برای این کار باید دو زاویه اندازه گیری شناخته شده را جمع کنید
تنها چیز مهمی که باید بدانید این است که مجموع زوایای یک مثلث همیشه 180 درجه می باشد. بنابراین، اگر دو مورد از سه اندازهگیری مثلث را بدانید، تنها یک قطعه از پازل را از دست دادهاید.
حتما بخوانید: فرمول مساحت مربع چیست؟
اولین کاری که شما می توانید انجام دهید این است که اندازه گیری های زاویه ای را که می دانید را اضافه کنید. در این مثال، دو اندازه گیری زاویه ای که می دانید 80 درجه و 65 درجه هستند. آنها را جمع کنید (80 درجه + 65 درجه) تا 145 درجه برای شما به دست آورید.
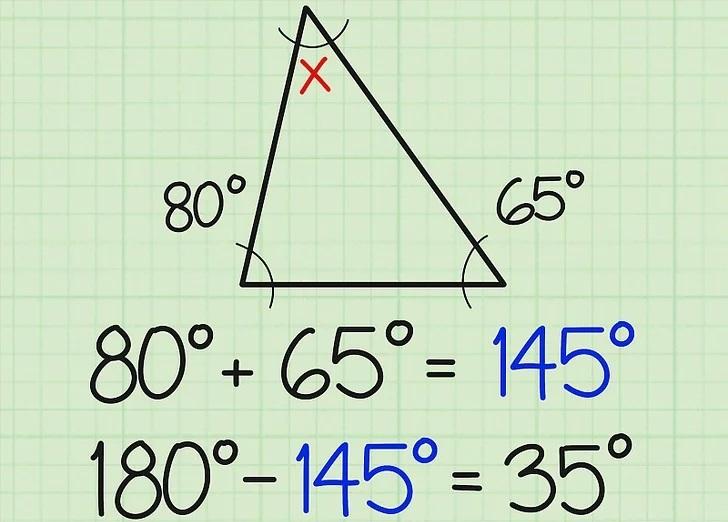
عدد 145 را از 180 درجه کم کنید. مجموع زوایای یک مثلث به 180 درجه می رسد. بنابراین، زاویه باقیمانده باید زوایا را تا 180 درجه جمع کند. در این مثال، 180 درجه - 145 درجه = 35 درجه.
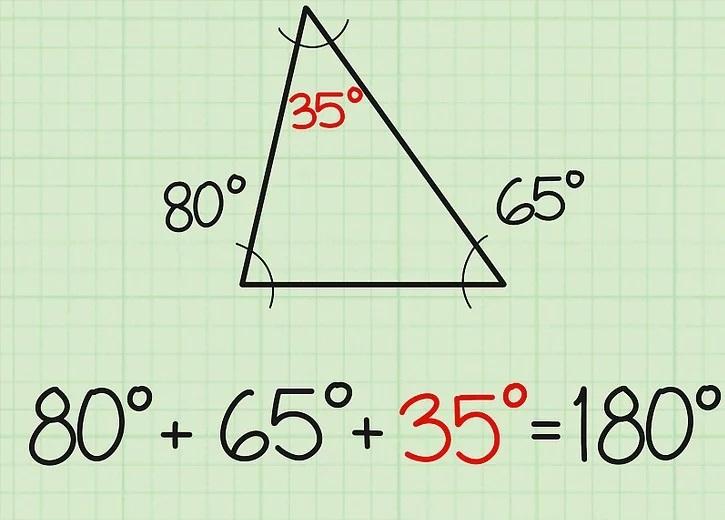
پاسخ خود را بنویسید. اکنون می دانید که زاویه سوم 35 درجه می باشد. اگر به خودتان شک دارید، فقط کار خود را بررسی کنید. سه زاویه باید تا 180 درجه جمع شوند تا مثلث بتواند وجود داشته باشد. 80 درجه + 65 درجه + 35 درجه = 180 درجه. خب درسته.
2. نحوه پیدا کردن زاویه سوم مثلث با استفاده از متغیرها
مسئله خود را یادداشت کنید. گاهی اوقات، به جای اینکه به اندازه کافی خوش شانس باشید که اندازه های دو تا از زاویه های یک مثلث را بدانید، فقط چند متغیر یا چند متغیر و یک زاویه اندازه گیری شده به شما داده می شود.
حتما بخوانید: روش محاسبه محیط مربع با مثال برای همه پایه ها
فرض کنید با این مسئله مواجهه شده اید: اندازه های زاویه x مثلثی را که اندازه های آن x و 2x و 24 است را پیدا کنید. ابتدا فقط آن را یادداشت کنید.
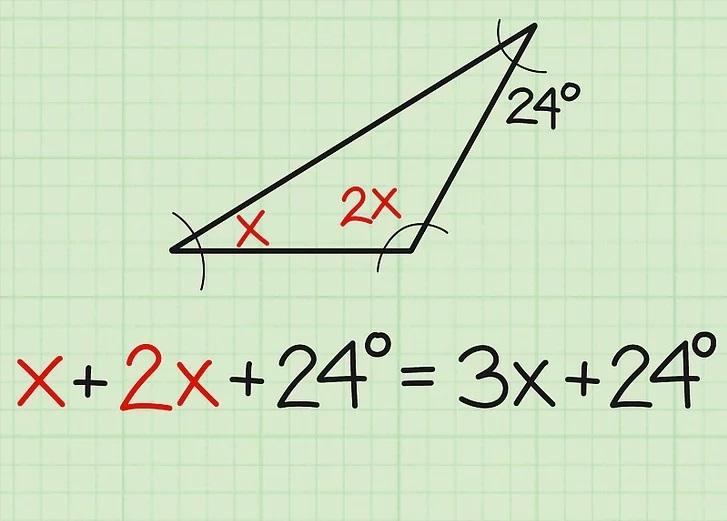
تمام اندازه گیری ها را جمع کنید. این همان اصلی است که اگر اندازه گیری دو زاویه را می دانستید از آن پیروی می کردید. به سادگی اندازه گیری زاویه ها را جمع آوری کرده و متغیرها را ترکیب کنید. پس بنابراین طبق گفته های من باید عبارتی شبیه به عبارت روبرو برای خود بنویسید: x + 2x + 24° = 3x + 24°.
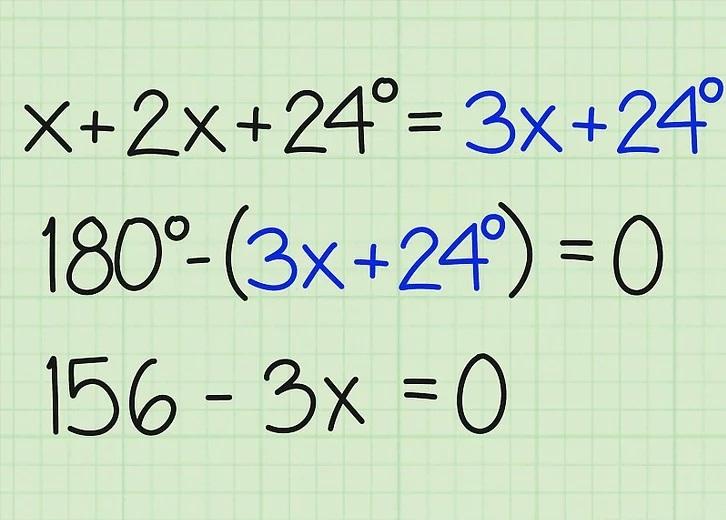
اندازه ها را از 180 درجه کم کنید. اکنون این اندازهها را از 180 درجه کم کنید تا به حل مشکل خود نزدیکتر شوید. حتماً اطمینان حاصل کنید که معادله خود را برابر با 0 قرار داده باشید. عبارات زیر را با دقت بررسی کنید.
- 180 درجه - (3x + 24 درجه) = 0
- 180 درجه - 3x - 24 درجه = 0
- 156 درجه - 3x = 0
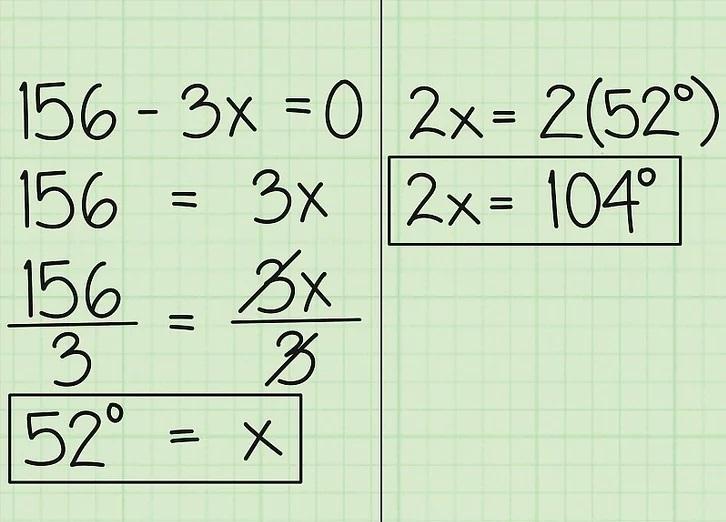
x را حل کنید. تنها کافیست متغیرها را در یک طرف معادله و اعداد را در طرف دیگر قرار دهید. 156 درجه = 3 برابر دریافت خواهید کرد. حالا هر دو طرف معادله را بر 3 تقسیم کنید تا x = 52 درجه باشد. این به این معنی است که زاویه اندازه گیری شده سوم مثلث 52 درجه است. زاویه دیگر 2x می شود 2 52x درجه یا 104 درجه.
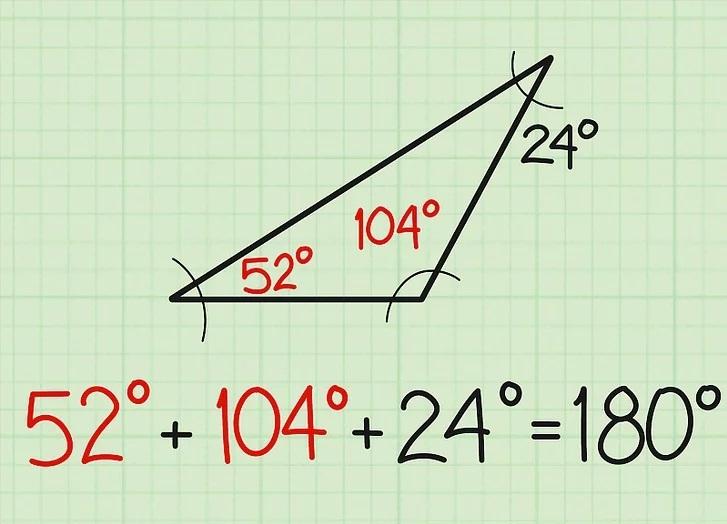
مسئله خود را چک کنید. اگر میخواهید مطمئن شوید که این یک مثلث معتبر از نظر زوایا می باشد، فقط کافیست که سه زاویه اندازهگیری شده را جمع کنید تا مطمئن شوید که مجموع آنها به 180 درجه میرسد یا نه. در اینجا 52 درجه + 104 درجه + 24 درجه = 180 درجه می شود.
3. نحوه پیدا کردن زاویه سوم مثلث با استفاده از روش های دیگر
حتما بخوانید: فرمول های مساحت اشکال هندسی مختلف
1. زاویه سوم مثلث متساوی الساقین را پیدا کنید
مثلث های متساوی الساقین دو ضلع مساوی و دو زاویه مساوی دارند. اضلاع مساوی با یک علامت هاش بر روی هر یک از آنها مشخص می شوند که نشان می دهد زوایای هر طرف با یک دیگر برابر هستند. اگر اندازه گیری زاویه یک زاویه مساوی از یک مثلث متساوی الساقین را بدانید، آنگاه اندازه گیری زاویه مساوی دیگر را بدون شک به دست خواهید آورد. اگر یکی از زوایای مساوی 40 درجه باشد، می دانید که زاویه دیگر نیز 40 درجه است. با کم کردن 40 + 40 درجه (که 80 درجه است) از 180 درجه می توانید ضلع سوم را در صورت نیاز پیدا کنید. 180 - 80 درجه = 100 درجه، که مقدار زاویه اندازه گیری شده باقی مانده می باشد.
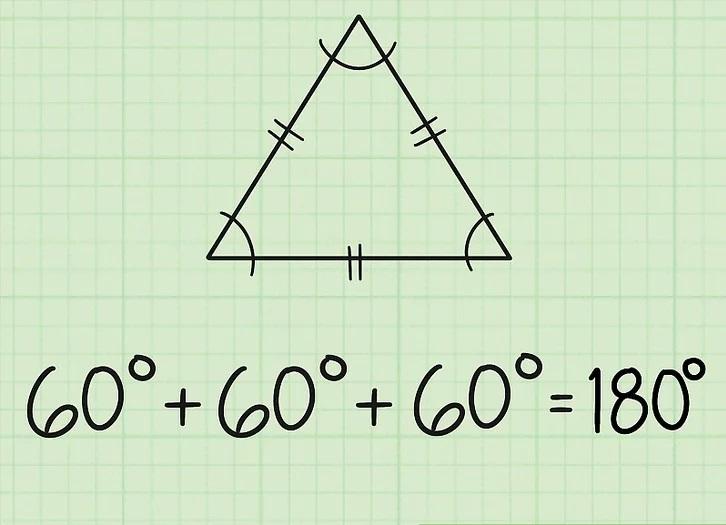
2. زاویه سوم مثلث متساوی الاضلاع را پیدا کنید
یک مثلث متساوی الاضلاع همه اضلاع و همه زوایا مساوی دارد که معمولاً با دو علامت هش در وسط هر یک از طرفین آن مشخص می شود. این بدان معنی است که اندازه گیری زاویه هر زاویه در یک مثلث متساوی الاضلاع 60 درجه است. مثلث خود را چک کنید. 60 درجه + 60 درجه + 60 درجه = 180 درجه.

3. زاویه سوم مثلث قائم الزاویه را پیدا کنید
فرض کنید می دانید که یک مثلث قائم الزاویه دارید که یکی از زوایای دیگر آن 30 درجه می باشد. اگر مثلث قائم الزاویه باشد، شما باید بدانید که یکی از زاویه ها دقیقاً 90 درجه است. برای این مثلث هم دقیقا همان اصول اعمال می شوند. تنها کاری که باید انجام دهید این است که اندازههای اضلاعی را که میشناسید (30 درجه + 90 درجه = 120 درجه) جمع کنید و آن عدد را از 180 درجه کم کنید. بنابراین، 180 درجه - 120 درجه = 60 درجه. زاویه اندازه گیری شده سوم این مثلث 60 درجه می باشد.
سخن آخر
مطالب مرتبط:
روش محاسبه محیط و مساحت ذوزنقه تصویری و به زبان ساده با مثال

دیدگاه ها