مسئلهٔ صفحهٔ 110 و 111 نمونهای کاربردی از بهکارگیری قضیهٔ فیثاغورس در زندگی روزمره است: وقتی عرض یک کانال و اختلاف سطح دو سو را داشته باشیم، طول پلی که این دو نقطه را به هم وصل میکند برابر وتر مثلث قائمالزاویهای خواهد بود که اضلاع قائمهاش همان عرض کانال و ارتفاع دیواره هستند. در این فعالیت، هم از فیثاغورس استفاده میکنیم و هم روش تقریبی برای بهدستآوردن جذر را مرور میکنیم تا مقدار وتر را تا دقت خواسته شده بیابیم. در این مقاله از سلام دنیا به حل فعالیت صفحهٔ 110 و 111 ریاضی پایهٔ هشتم همراه با توضیح روشها و تقریب عددی مقدار جذر تا دو رقم اعشار پرداختهایم.
حل فعالیت صفحه 110 ریاضی هشتم با جواب
آزاده، نرگس و نسیم هنگام گردش علمی به یک آب گذر (کانال) به عرض 5 متر رسیدند. در طرف دیگر آب گذر دیوارهای به ارتفاع 3 متر وجود داشت. آنها میخواهند بدانند اگر پلی برای رفتن به طرف دیگر آب ساخته شود، طول آن چقدر خواهد بود؟

در ادامه، گفت و گوی این سه دانش آموز را می خوانید که برای حل این مسئله صورت گرفته است. با دقت در این گفت و گو سعی کنید نظر هر دانش آموز را توضیح دهید.
حتما بخوانید: حل سوالات صفحه 111 تا 113 ریاضی هشتم
- آزاده: به نظر من این مسئله مانند آن است که یک مثلث قائم الزاویه به اضلاع 3 و 5 متر داشته باشیم و بخواهیم وتر آن را به دست آوریم.
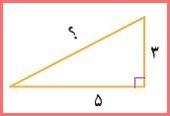
- نرگس: پس میتوانیم از رابطه فیثاغورس استفاده کنیم.
- نسیم: یعنی رابطه مقابل را داریم: 34 = 32 + 52 مربع وتر
- آزاده: درست است. اکنون برای به دست آوردن طول وتر باید جذر عدد 34 را به دست آوریم.
- نرگس: چون 36 > 34 > 25 پس 34√ بین دو عدد 5 و 6 قرار دارد.
یعنی داریم: 6 > √34 > 5

- نسیم: اگر فاصله 5 تا 6 را روی محور نصف کنیم، عدد 5/5 به دست میآید و چون 30/25 = 2(5/5) ، پس حتماً جذر 34 از 5/5 بیشتر است.
- آزاده: می توانیم چند عدد بزرگتر از 5/5 را بررسی کنیم؛ مثلاً 5/7 و 5/8 و 5/9.

سپس آنها به کمک ماشین حساب جدول زیر را تکمیل کردند.

در نتیجه با توجه به جدول بالا، مقدار 34√ تقریباً برابر 5/8 است. آخرین جمله فعّالیت بالا را معمولاً به شکل زیر مینویسیم:
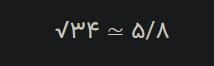
اگر این دانش آموزان بخواهند به کمک روش بالا مقدار 34√ را تا دو رقم اعشار حساب کنند، چگونه باید این کار را انجام دهند؟
حتما بخوانید: حل سوالات صفحه 114 ریاضی هشتم
- با توجه به جدول زیر پاسخ را به دست میآوریم:

مقدار 34√ تا پنج رقم اعشار به کمک ماشین حساب چنین به دست میآید:
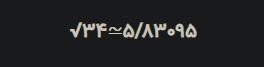
//////////////////////////////////////////////////////////////
ویدئو آموزش و حل صفحه 110 و 111 ریاضی هشتم
ویدئو آموزش و حل صفحه 110 و 111 ریاضی هشتم
سخن آخر
این فعالیت نشان میدهد که ترکیب مدل هندسی (قضیهٔ فیثاغورس) و روشهای تقریبی (جستوجوی اعشاری یا استفاده از ماشینحساب) چگونه طول اجسام واقعی را با دقت دلخواه تعیین میکند. تسلط بر این روشها نهتنها در مسائل هندسی کتاب، بلکه در محاسبات عملی مهندسی و زندگی روزمره بسیار سودمند است.
مطالب مرتبط:
ساخت کاردستی با آرمیچر برای مدرسه
42 نقاشی دفاع مقدس و شهیدان کلاس اول تا ششم
8 انشا در مورد گذشت و فداکاری با مقدمه و نتیجه


دیدگاه ها