در این بخش از کتاب ریاضی هشتم، مفهوم رابطه بین زاویههای داخلی و خارجی چندضلعیها آموزش داده میشود. دانشآموز یاد میگیرد که چگونه با دانستن چند زاویه، زاویههای دیگر را محاسبه کند و همچنین متوجه میشود که مجموع زاویههای خارجی در هر چندضلعی همواره مقدار ثابتی دارد. در این مقاله از سلام دنیا به حل کامل فعالیت و کار در کلاس صفحه 48 ریاضی هشتم با پاسخ تشریحی و توضیح دلیل هر رابطه هندسی پرداختهایم.
حل کار در کلاس صفحه 48 ریاضی هشتم با جواب
سوال 2 صفحه 48 ریاضی پایه هشتم با توضیح
2. اندازهٔ دو زاویهٔ یک مثلث را میدانیم؛ پس میتوانیم اندازهٔ زاویهٔ سوم آن را پیدا کنیم. (چگونه؟)
- جواب: مجموع دو زاویه را محاسبه کرده و از 180 کم میکنیم.
حتما بخوانید: حل تمرین صفحه 49 ریاضی هشتم
برای اینکه بتوانیم اندازهٔ همهٔ زاویههای هر یک از شکلهای زیر را پیدا کنیم، دست کم چندتا از آنها باید معلوم باشند؟
- الف) لوزی ==> یک زاویه
ب) چهارضلعی با ضلعهای نامساوی ==> سه زاویه

///////////////////////////////////////////////////////////
حل فعالیت صفحه 48 ریاضی هشتم با جواب
سطر اول جدول زیر، نشان میدهد که مجموع زاویههای خارجی یک مثلث برابر °360 است.
- الف) جدول را کامل کنید و مجموع زاویههای خارجی شکلهای بعدی را به دست آورید.
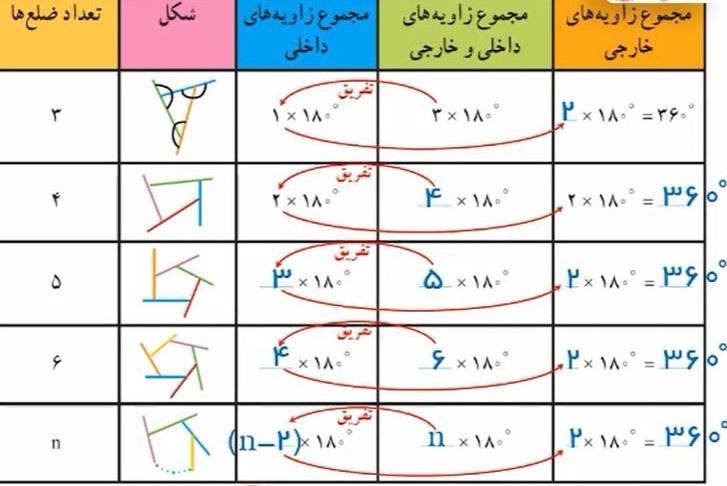
- حاصل تفریق =n−(n−2)=n−n+2=2=n−(n−2)=n−n+2=2
ب) فکر میکنید مجموع زاویههای خارجی یک هفت ضلعی چند درجه است؟
- مجموع زاویههای خارجی هر چند ضلعی، 360 درجه است.
یک هشت ضلعی چطور؟
- 360 درجه
///////////////////////////////////////////////////////////
ویدئو آموزش و حل صفحه 48 ریاضی هشتم
ویدئو آموزش و حل صفحه 48 ریاضی هشتم
سخن آخر
درک رابطه میان زاویههای داخلی و خارجی چندضلعیها به دانشآموز کمک میکند تا ساختار اشکال هندسی را بهتر بشناسد و در محاسبه و اثبات روابط هندسی دقت بیشتری داشته باشد. این مفهوم پایهای در ادامه مباحث هندسه بسیار کاربرد دارد.
مطالب مرتبط:
چگونه زاویه مثلث را پیدا کنیم؟
60 نقاشی حاشیه دفتر مشق جدید آسان پاییزی با مداد رنگی دخترانه و پسرانه


دیدگاه ها