چگونه مسائل ریاضی را ساده کنیم؛ راهبردهای حل مسئله ریاضی با مثال

در ریاضی، وقتی از دانش‌آموزان خواسته می‌شود پاسخ‌های خود را به «ساده‌ترین عبارت» بنویسند، یعنی باید آن‌ها را به کوچک‌ترین و خلاصه‌ترین شکل ممکن تبدیل کنند. تا وقتی که یک مسئله به ساده‌ترین حالت خودش نرسد، حل‌شده حساب نمی‌شود. ما در این مطلب از سلام دنیا، به شما یاد می‌دهیم که راهبردهای حل مسئله ریاضی با مثال چیست و چطور از عبارات ساده شروع کنید و بعد به سراغ حل معادلات پیچیده بروید. با ما همراه باشید.

نکته مهم: توجه کنید که علامت ^  در عبارات ها به معنای توان است. مثلا 2^3 به معنای (عدد 3 به توان 2 است)

راهبردهای حل مسئله ریاضی با مثال

اول، هر چیزی که داخل پرانتز هست رو حل کن. بعد، توان‌ها رو با هم ضرب کن. بعد از اون، تمام چیزهایی که با هم یکسان هستن رو با هم ضرب کن.

روش1 : ساده سازی عبارات پایه

1. از ترتیب عملیات استفاده کنید

وقتی می‌خوای یک عبارت رو ساده کنی، نمی‌تونی از چپ به راست بری. باید ترتیب کارها رو رعایت کنی. اگه کارها رو به ترتیب انجام ندی، ممکنه جواب اشتباه بشه. یک کلمه‌ی خوب که می‌تونی برای یادآوری ازش استفاده کنی، «PEMDAS» هست. ترتیب کارها به این صورته:

حتما بخوانید: فعال سازی نرم افزار و نوشتن فرمول ریاضی در ورد گوشی

• پرانتز
• توان
• ضرب
• تقسیم
• جمع
• تفریق

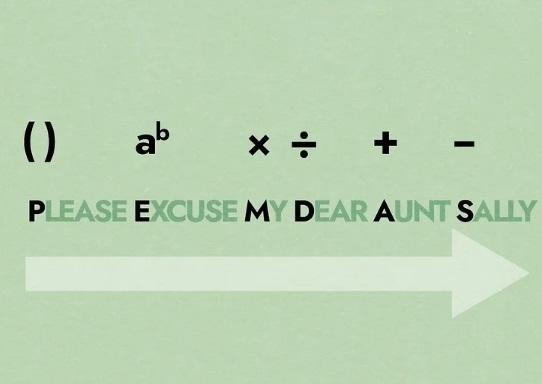
2. تمام عبارات داخل پرانتز را حل کنید

در ریاضیات، پرانتز نشان می دهد که عبارت های داخل باید جدا از عبارت اطراف محاسبه شوند. قبل از انجام هر کار دیگری، شرایط داخل پرانتز را بررسی کنید. توجه داشته باشید که ترتیب عملیات همچنان در داخل هر جفت پرانتز اعمال می شود.

• به عنوان مثال، در داخل پرانتز، باید قبل از جمع، تفریق و غیره ضرب کنید به عنوان مثال، بیایید سعی کنیم عبارت "2x + 4(5 + 2) + 3^2 - (3 + 4/2)" را ساده کنیم . در این عبارت ابتدا عبارت های داخل پرانتز "2+5" و " 4/2+ 3" را حل می کنیم. "5= 2+3 = 4/2+ 7.3 = 2+5"

حتما بخوانید: آموزش پیدا کردن زاویه بین 2 بردار با فرمول ضرب داخلی و خارجی

• عبارت پرانتزی دوم به 5 ساده می شود، زیرا به دلیل ترتیب عملیات، 4/2 را به عنوان اولین عمل خود در داخل پرانتز تقسیم می کنیم. اگر به سادگی از چپ به راست برویم، ممکن است ابتدا 3 و 4 را اضافه کنیم، سپس بر 2 تقسیم کنیم و پاسخ نادرست 7/2 را بدهیم.
• توجه به پرانتزهای متعدد: اگر چند پرانتز در داخل یکدیگر وجود دارد، ابتدا درونی‌ترین عبارت‌ها را حل کنید، سپس دومین و غیره را حل کنید.

3. برای حل هر توان ضرب کنید

بعد از اینکه پرانتزها رو حل کردی، توان عبارت خودت رو حل کن. توان‌ها اعداد کوچکی هستند که درست کنار عدد بزرگ‌تر (به نام عدد پایه) نوشته می‌شوند. با ضرب کردن، جواب هر کدوم از توان‌ها رو پیدا کن، سپس جواب‌ها رو به جای خودشون در معادله قرار بده. 

• پس از پرداختن به پرانتز، عبارت مثال ما اکنون "2x + 4(7) + 3^2 - 5" است . تنها توان در مثال ما 3 به توان 2 است ، بنابراین ما 3 را در خودش ضرب می کنیم (یعنی 3x3)، که برابر با 9 است . این را دوباره به معادله در جای 3 به توان 2 اضافه کنید تا "2x + 4(7) + 9 - 5" به دست آید.

4. مسائل ضرب را در عبارت خود حل کنید

بعد، تمام ضرب در عبارت خود را انجام دهید. به یاد داشته باشید که ضرب را می توان به روش های مختلفی نوشت. نماد بار (×)، نقطه (⋅)، یا ستاره (*) همه راه هایی برای نشان دادن ضرب هستند. یک عدد در آغوش پرانتز یا یک متغیر (مانند (x) 4) نیز به این معنی است که شما ضرب می کنید.

حتما بخوانید: فرمول محیط مربع چیست

• دو نمونه از ضرب در مسئله ما وجود دارد: "( × 2x هست×2)2x" . ما مقدار x را نمی دانیم، بنابراین "28=7 × 4=(7)4" را حل می کنیم . می توانیم معادله خود را به صورت "2x + 28 + 9 - 5" بازنویسی کنیم .

5. هر تقسیمی را که باید انجام دهید کامل کنید

همانطور که برای مسائل تقسیم در عبارت خود جستجو می کنید، به خاطر داشته باشید که، مانند ضرب، تقسیم را می توان به چند روش نوشت. نماد ساده ÷ یک است، اما به یاد داشته باشید که اسلش ها و میله ها در یک کسری (مثلاً 3/4 ) نشان می دهد که باید تقسیم کنید.

• از آنجایی که ما قبلاً یک مشکل تقسیم (4/2) را در هنگام برخورد با اصطلاحات داخل پرانتز حل کرده‌ایم، در مثال ما دیگر هیچ تقسیمی در آن وجود ندارد، بنابراین از این مرحله می‌گذریم. این یک نکته مهم را نشان می دهد - شما مجبور نیستید هر عملیات را در مخفف PEMDAS هنگام ساده کردن یک عبارت انجام دهید. شما فقط باید مراحلی را که در مسئله شما وجود دارد را کامل کنید.

6. هر عددی را که باید ترکیب شود اضافه کنید

بعد، هر جمعی که نیاز داری رو انجام بده. می‌تونی به سادگی از چپ به راست به عبارتی که داری ادامه بدی، اما ممکنه بهتر باشه اول اعدادی رو که به روش‌های ساده و راحت ترکیب می‌شوند، اضافه کنی. برای مثال، در عبارت "71+51+29+49" ، آسون‌تره که اول "100 = 51 + 49" انجام بدین ، بعد "100 = 71+ 29" و در نهایت رو "200 = 100 + 100" به دست بیاری، تا اینکه بخوای "78=29+49" و "129=51+78" و "200= 71+129" رو انجام بدی و حساب کنی.

حتما بخوانید: آموزش رسم زاویه 30 درجه با خط کش و پرگار

• عبارت مثالی ما به طور جزئی ساده شده و به شکل "2x + 28 + 9 - 5" درآمده. حالا باید جمع‌هایی که می‌تونیم رو انجام بدیم، بنابراین از چپ به راست به هر جمع نگاه می‌کنیم. نمی‌تونیم 2x و 28 رو جمع کنیم چون ارزش x رو نمی‌دونیم، پس می‌ریم سراغ "37= 9+28". بعد می‌تونیم عبارت خودمون رو به شکل "2x + 37 - 5" بنویسیم.

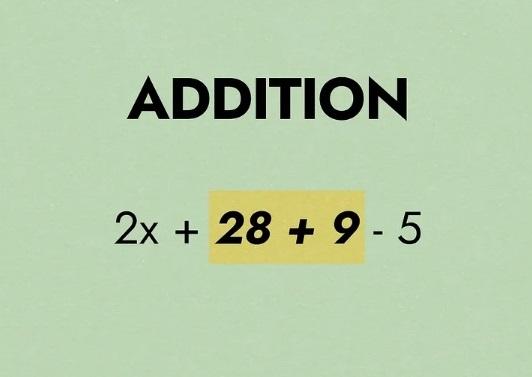
7. هرجا که نیاز داری، تفریق کن

آخرین مرحله در "PEMDAS" تفریق هست. از طریق مشکلت پیش برو و هر مشکل تفریقی که باقی مونده رو حل کن. می‌تونی در این مرحله به جمع اعداد منفی هم بپردازی، یا در همون مرحله‌ای که جمع‌های معمولی رو انجام می‌دی (این به جواب تو تأثیری نمی‌ذاره).

• در عبارت ما، "2x + 37 - 5"، فقط یک مشکل تفریق داریم. "32= 5 -37"

8. بیان خود را مرور کنید و هر عبارت باقی مانده را ترکیب کنید

پس از انجام ترتیب عملیات، عبارت خودت رو با ساده‌ترین شکل باقی می‌ذاری. اما اگر عبارت تو یک یا چند متغیر داشته باشه، اصطلاحات متغیر تا حد زیادی دست نخورده باقی می‌مونن. برای ساده کردن عبارات متغیر، باید مقادیر متغیرهای خودت رو پیدا کنی یا از تکنیک‌های خاصی برای ساده کردن عبارت استفاده کنی.

• پاسخ نهایی ما "2x + 32" هست. تا زمانی که مقدار x رو ندانیم، نمی‌تونیم به جمع نهایی این مشکل بپردازیم، اما وقتی بفهمیم x چه مقداری داره، حل این عبارت خیلی آسون‌تر از عبارت طولانی اولیه ما خواهد بود.

حتما بخوانید: فرمول های "مساحت "و "مساحت کل" اشکال هندسی مختلف

• نکته ای در مورد ترکیب عبارت ها: اگر معادله ای دارید که در آن عبارت های مشابه وجود دارد، اکنون زمانی است که آنها را ترکیب می کنید.
• فرض کنید ما با "2x + 32 + 4x + 12 = y" مانده ایم. ما می‌توانیم 32 و 12 و 2x و 4x را با هم ترکیب کنیم تا "6x + 44 = y" را به‌عنوان عبارت ساده شده نهایی خود به دست آوریم.

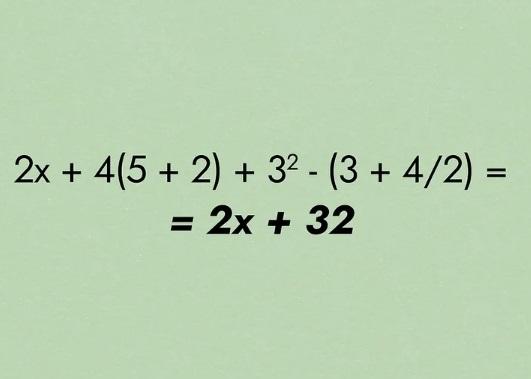
روش 2: ساده سازی عبارات پیچیده

1. همه اصطلاحات متغیر مانند خود را با هم ترکیب کنید

هنگام برخورد با عبارات متغیر، مهم است که به یاد داشته باشید که عبارت‌های دارای متغیر و توان یکسان (معروف به اصطلاحات مشابه ) می‌توانند مانند اعداد عادی اضافه و کم شوند. عبارت ها نه تنها باید متغیر یکسانی داشته باشند، بلکه باید یک توان نیز داشته باشند. به عنوان مثال، 7x و 5x را می توان به یکدیگر اضافه کرد، اما 7x و 2^5x را نمی توان.

• این قانون به اصطلاحات دارای متغیرهای متعدد نیز گسترش می یابد. به عنوان مثال، "2xy^2" را می توان به "2^3xy- " اضافه کرد ، اما نه "3x^2y-" یا "2^3y-".
• بیایید به عبارت "x^2 + 3x + 6 - 8x" نگاه کنیم. در این عبارت می‌توانیم عبارت‌های "3x" و "8x-" را اضافه کنیم زیرا آنها مانند عبارت‌ها هستند. ساده شده، عبارت ما "x^2 - 5x + 6" است .

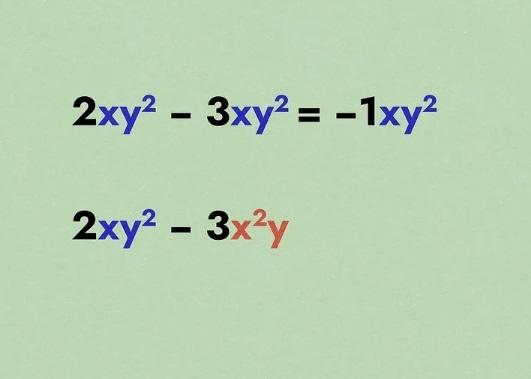
2. کسرهای عددی را با تقسیم یا "لغو" فاکتورها ساده کنید

کسری هایی که هم در صورت و هم در مخرج فقط عدد دارند (و هیچ متغیری ندارند) را می توان به چند روش ساده کرد. ساده ترین راه برای ساده کردن در اینجا این است که به سادگی کسری را به عنوان یک مسئله تقسیم در نظر بگیرید و صورت را بر مخرج تقسیم کنید. علاوه بر این، هر عامل ضربی که هم در صورت و هم در مخرج ظاهر می شود را می توان "لغو" کرد زیرا آنها با تقسیم عدد 1 را به دست می آورند. به عبارت دیگر،اگر صورت و مخرج هر دو در یک عامل مشترک باشند، این عامل می تواند از ضریب حذف شود. کسری، یک پاسخ ساده باقی می ماند.

حتما بخوانید: دانلود 8 برنامه اندازه گیری، قد، مساحت برای گوشی

• برای مثال، کسری 36/60 را در نظر می گیریم. اگر یک ماشین حساب دستی داشته باشیم، می توانیم تقسیم کنیم تا پاسخ 0.6 به دست آید . با این حال، اگر این کار را نکنیم، باز هم می‌توانیم با حذف عوامل رایج کار را ساده کنیم. تصویر 36/60 به عنوان "(10 × 6)/(6 × 6)" . این را می توان به صورت "1=6.6 .6/10 ×6/6" بازنویسی کرد. بنابراین عبارت ما در واقع "6/10= 6/10 × 1" است. با این حال، ما هنوز تمام نشده‌ایم - هر دو 6 و 10 ضریب 2 را به اشتراک می‌گذارند. با تکرار روش بالا، ما با 3/5 باقی می‌مانیم .
• شما باید هم صورت و هم مخرج را بر بزرگترین عامل مشترک آنها تقسیم کنیدکه در مثال بالا 12 برابر است: "(5× 12)/(3× 12)"

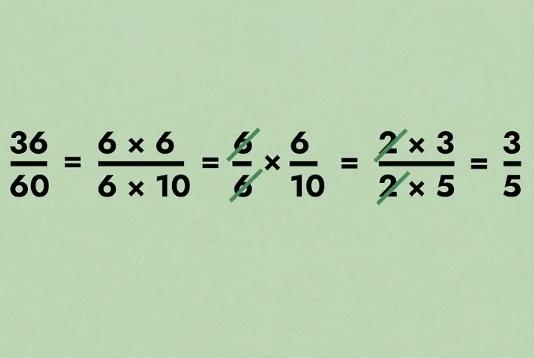
3. در کسرهای متغیر، عوامل متغیر را لغو کنید

عبارات متغیر در قالب کسری فرصت های منحصر به فردی را برای ساده سازی ارائه می دهند. مانند کسرهای معمولی، کسرهای متغیر به شما این امکان را می‌دهند که عواملی را که هم با صورت و هم مخرج مشترک هستند حذف کنید. با این حال، در کسرهای متغیر، این عوامل می توانند هم اعداد و هم عبارات متغیر واقعی باشند.

• بیایید عبارت "(3x^2 + 15x-)/ (3x^2 + 3x)" را در نظر بگیریم. این کسر را می توان به صورت "(x-5)(3x)/(3x)(x + 1)" بازنویسی کرد، زیرا 3x هم در صورت و هم در مخرج ظاهر می شود. با حذف این عوامل از معادله "(5 - x)/ (x + 1)" برگ می شود . به همین ترتیب، در عبارت "2/(2x^2 + 4x + 6)"، هر جمله بر 2 بخش پذیر است، بنابراین می توانیم عبارت را به صورت "2/((x^2 + 2x + 3)2)" بنویسیم و بنابراین به " 3 + x^2 + 2x " ساده کنیم .
• توجه داشته باشید که نمی‌توانید هر عبارتی را لغو کنید—فقط می‌توانید عوامل ضربی را که هم در صورت و هم در مخرج ظاهر می‌شوند، لغو کنید. به عنوان مثال، در عبارت "ایکس /(x(x + 2))" از صورت و مخرج حذف می شود و "(x + 2)= یک/(x + 2)" باقی می ماند. با این حال، "ایکس/(x + 2)" به "2= 2/1" لغو نمی شود .

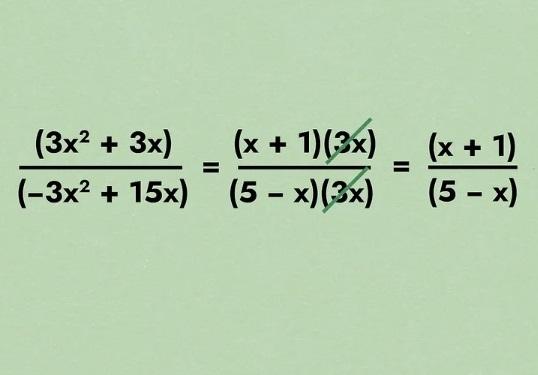
4. عبارت های پرانتزی را در ثابت های آنها ضرب کنید

 هنگامی که با عبارت های متغیر داخل پرانتز با یک ثابت مجاور سروکار داریم، گاهی اوقات، ضرب هر عبارت داخل پرانتز در ثابت می تواند به بیان ساده تری منجر شود. این برای ثابت های عددی محض و برای ثابت هایی که شامل متغیرها هستند صادق است.

حتما بخوانید: روش محاسبه محیط و مساحت ذوزنقه

• به عنوان مثال، عبارت  "(x^2 + 8) 3" را می توان به "3x^2 + 24" ساده کرد ، در حالی که "3x (x^2 + 8)" را می توان به "3x^3 + 24x" ساده کرد .
• توجه داشته باشید که در برخی موارد، مانند کسرهای متغیر، ثابت مجاور پرانتز فرصت لغو را می دهد و بنابراین نباید از طریق پرانتز ضرب شود. در کسر "(3 ایکس/(x^2 + 8)3)"، ضریب 3 هم در صورت و هم در مخرج ظاهر می‌شود، بنابراین می‌توانیم آن را لغو کنیم و عبارت را به "ایکس/(x^2 + 8)" ساده کنیم . کار کردن با این ساده‌تر و آسان‌تر از "3 ایکس/(3x^3 + 24x)" است، که اگر ضرب می‌کردیم جوابی می‌گرفتیم.

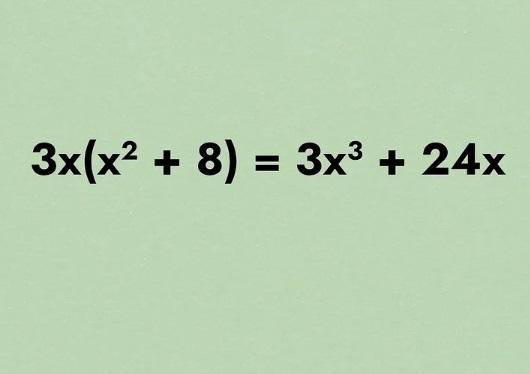
5. با فاکتورسازی ساده کنید

فاکتورینگ تکنیکی است که با آن می توان برخی از عبارات متغیر از جمله چند جمله ای ها را ساده کرد. فاکتورگیری را برعکس مرحله «ضرب از طریق پرانتز» در بالا در نظر بگیرید—گاهی اوقات، یک عبارت را می‌توان ساده‌تر به‌عنوان دو عبارت ضرب شده در یکدیگر، نه به‌عنوان یک عبارت واحد، ارائه کرد. این امر به ویژه در صورتی صادق است که فاکتورگیری یک عبارت به شما امکان دهد بخشی از آن را لغو کنید (همانطور که در کسری انجام می دهید). در موارد خاص (اغلب با معادلات درجه دوم)، فاکتورگیری حتی به شما امکان می دهد پاسخ معادله را بیابید.

• بیایید یک بار دیگر عبارت "x^2 - 5x + 6" را در نظر بگیریم. این عبارت می تواند به "(x - 2) (x - 3)" فاکتور شود. بنابراین، اگر "x^2 - 5x + 6" ، صورت‌دهنده یک عبارت خاص با یکی از این عبارات عامل در مخرج باشد، مانند عبارت "((x - 2)2)/(x^2 - 5x + 6)" ، ممکن است بخواهیم آن را به صورت فاکتور بنویسیم تا بتوانیم آن را با مخرج لغو کنیم. به عبارت دیگر، با "((x - 2)2)/(x - 2) (x - 3)" ، شرایط "(x - 2)" لغو می‌شوند و "2/(x - 3)" را برای ما باقی می‌گذارند .
• دلیل دیگری که ممکن است بخواهید بیان خود را فاکتور بگیرید این است که فاکتورگیری می تواند پاسخ معادلات خاصی را نشان دهد. بیایید معادله "x^2 - 5x + 6 = 0" را در نظر بگیریم. فاکتورسازی ما را به دست می‌آورد "0=(x - 2) (x - 3)". از آنجایی که هر عدد ضربدر صفر برابر با صفر است، می‌دانیم که اگر بتوانیم یکی از شرایط پرانتز را بدست آوریم. برای مساوی صفر، کل عبارت در سمت چپ علامت تساوی نیز برابر با صفر خواهد بود. بنابراین، 3 و 2 دو پاسخ به معادله هستند.

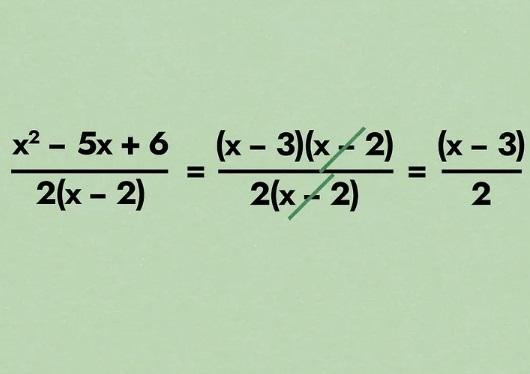
سخن آخر

ساده‌سازی مسائل ریاضی، یکی از مهارت‌های اساسی در یادگیری ریاضی است که به دانش‌آموزان کمک می‌کند تا عبارات پیچیده را به شکل‌های قابل فهم‌تری درآورند. با رعایت ترتیب عملیات و دقت در حل پرانتزها، توان‌ها، ضرب‌ها و جمع‌ها، می‌توان به راحتی به نتایج درست دست یافت. یادگیری این مهارت نه تنها در ریاضی، بلکه در حل مسائل روزمره نیز مفید خواهد بود.

مطالب مرتبط:

چگونه زاویه مثلث را پیدا کنیم؟

فرمول و روش محاسبه مساحت زمین