اگر در کلاس ریاضی در مورد زوایا و بردارها یاد میگیرید، احتمالاً معلمتان برای پیدا کردن زاویه بین 2 بردار به شما مسائلی را داده است. قطعا شروع به کار کمی گیج کننده به نظر می رسد، به همین دلیل است که ما اینجا هستیم تا به شما کمک کنیم! در این مطلب از سلام دنیا ، ما در مورد پیدا کردن زاویه بین 2 بردار ؛ فرمول یافتن زاویه بین 2 بردار را پیدا می کنند و نحوه استفاده از ضرب داخلی و خارجی را به شما آموزش می دهیم. برای حل مسائل ریاضی خود ادامه دهید!
فرمول یافتن زاویه بین 2 بردار
- برای یافتن زاویه بین بردارها با استفاده از حاصل ضرب اسکالر از فرمول
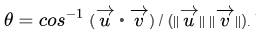 استفاده کنید.
استفاده کنید. - برای محاسبه حاصل ضرب اسکالر، مختصات جهت یکسان هر بردار را ضرب کرده و نتایج را با هم جمع کنید.
حتما بخوانید: فرمول و روش محاسبه مساحت زمین
- سپس، قدر هر بردار را با استفاده از قضیه فیثاغورث یا
 بیابید. برای بدست آوردن زاویه حاصل ضرب اسکالر از یک ماشین حساب استفاده کنید.
بیابید. برای بدست آوردن زاویه حاصل ضرب اسکالر از یک ماشین حساب استفاده کنید. - برای بدست آوردن زاویه بین بردارها از فرمول متقابل استفاده کنید.
روش 1: با استفاده از فرمول محصول نقطه
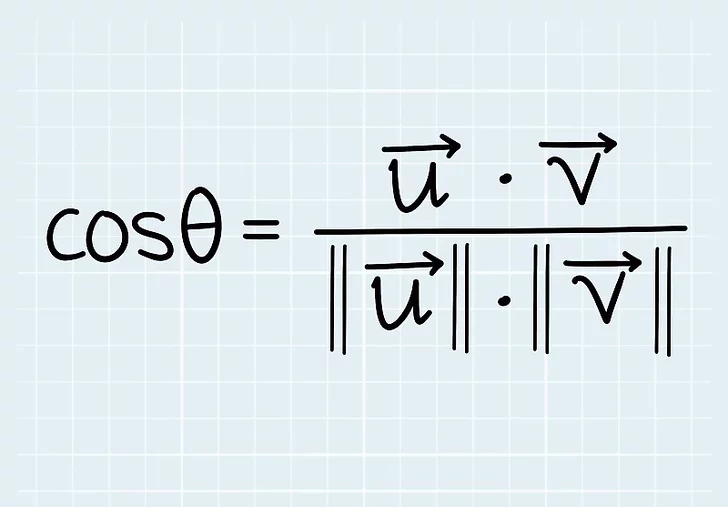
1. از فرمول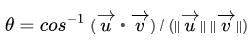 استفاده کنید. زاویه بین 2 بردار جایی است که دنباله های 2 بردار یا پاره خط به هم می رسند. هر بردار دارای یک قدر یا طول و جهتی است که در جهت آن است. بنابراین، برای یافتن زاویه بین 2 بردار، از فرمول بالا استفاده می کنید که در آن:
استفاده کنید. زاویه بین 2 بردار جایی است که دنباله های 2 بردار یا پاره خط به هم می رسند. هر بردار دارای یک قدر یا طول و جهتی است که در جهت آن است. بنابراین، برای یافتن زاویه بین 2 بردار، از فرمول بالا استفاده می کنید که در آن:
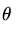 زاویه بین بردارها است.
زاویه بین بردارها است.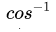 معکوس کسینوس یا قوس cos است.
معکوس کسینوس یا قوس cos است.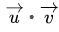 و u حاصل ضرب اسکالر بردار v است.
و u حاصل ضرب اسکالر بردار v است. و u قدر بردار v است.
و u قدر بردار v است.

2. مختصات بردارها را در مسئله ریاضی خود مشخص کنید
اکثر مسائل ریاضی مختصات ابعادی هر بردار را به شما می دهند که گاهی اوقات مولفه نیز نامیده می شود. شما از مختصات هر بردار برای یافتن بزرگی و حاصل ضرب نقطه ترکیبی آنها استفاده می کنید. اگر مسئله ریاضی شما از قبل قدر بردارها را نشان می دهد، از مرحله زیر بگذرید.
- به عنوان مثال، زاویه بین بردار را پیدا کنید. بردارu دارای مختصات(2و2) و بردار v دارای مختصات (0، 3).
- گاهی اوقات، بردارها به صورت نوشته می شوند
 و
و 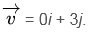
- در حالی که مثال ما از بردارهای دو بعدی استفاده می کند، یافتن زاویه بین بردارهای سه بعدی از همان مراحل پیروی می کند.
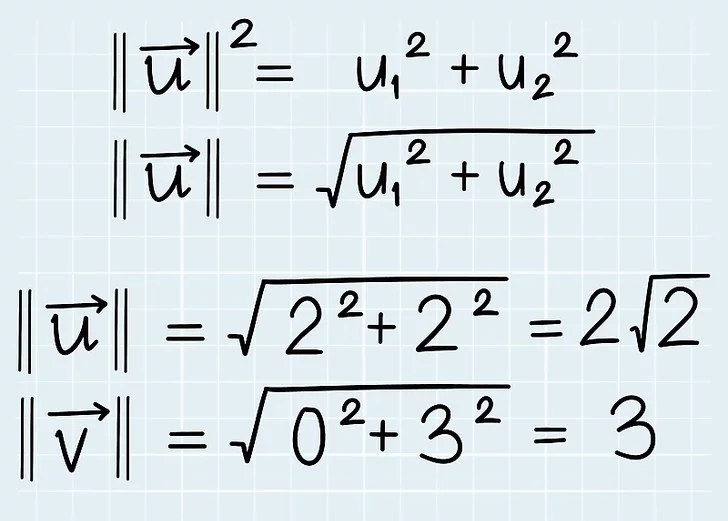
3. قدر هر بردار را محاسبه کنید
مثلث قائم الزاویه ای را تصویر کنید که از مؤلفه x بردار، مؤلفه y آن و خود بردار گرفته شده است. بردار مثلث را تشکیل می دهد، بنابراین برای یافتن قدر آن، به سادگی از قضیه فیثاغورث استفاده کنید . فقط مختصات هر بردار را به قضیه وصل کنید.
- در قضیه فیثاغورث a 2 + b 2 + c 2 ، قدر بردار با c نشان داده می شود. بنابراین، فقط معادله را بازنویسی کنید تا قدر از یک طرف جدا شود:
 و
و 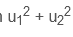 مختصات x و y بردار است.
مختصات x و y بردار است.
حتما بخوانید: فرمول های "مساحت "و "مساحت کل" اشکال هندسی مختلف
- با استفاده از مثال ما، قدر بردار u را در (2، 2) پیدا کنید و بردار v در (0، 3).
- u درج کنید مختصات در قضیه:
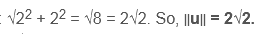 .
. - جواب
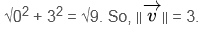 پیدا کنید . بنابراین،3= |v| .
پیدا کنید . بنابراین،3= |v| . - اگر یک بردار 3 بعدی است یا بیش از 2 جزء دارد، به سادگی به اضافه کردن
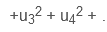 به قضیه فیثاغورث ادامه دهید.
به قضیه فیثاغورث ادامه دهید.
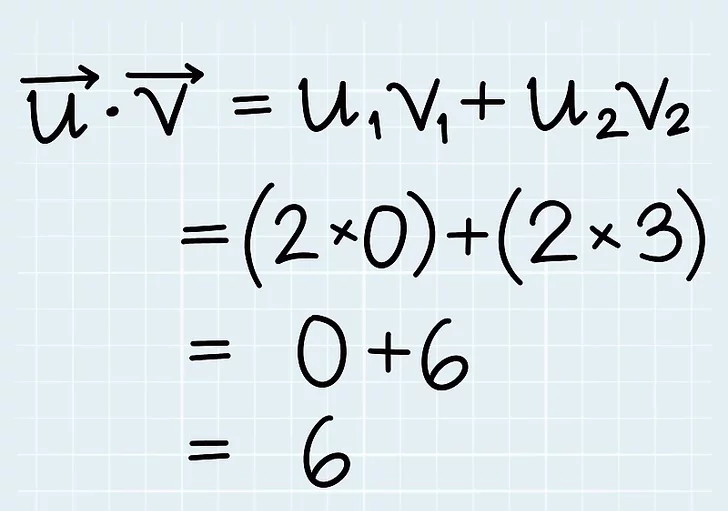
4. حاصل ضرب نقطه ای 2 بردار را محاسبه کنید
حاصل ضرب نقطه ای روشی برای ضرب بردارها است که معمولاً به آن حاصل ضرب اسکالر نیز می گویند .برای محاسبه حاصل ضرب نقطه، مختصات یکسان بردارها را ضرب کنید، سپس نتایج را با هم جمع کنید.
- برای برنامه های گرافیکی کامپیوتری، قبل از ادامه به نکاتی مراجعه کنید.با استفاده از مثال ما =u= (2، 2) v = (0، 3).
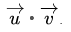 را پیدا کنید.
را پیدا کنید. - مختصات x را در u و v ضرب کنیدو مختصات
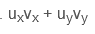 6=6+0=(2)(0) + (2)(3)
6=6+0=(2)(0) + (2)(3) - 6 حاصل ضرب اسکالر u و v است.
تعریف محصول نقطه ای
از نظر ریاضی مختصات بردار u هستند. اگر بردار شما بیش از 2 جزء دارد، به سادگی به اضافه کردن
مختصات بردار u هستند. اگر بردار شما بیش از 2 جزء دارد، به سادگی به اضافه کردن  ادامه دهید .
ادامه دهید .
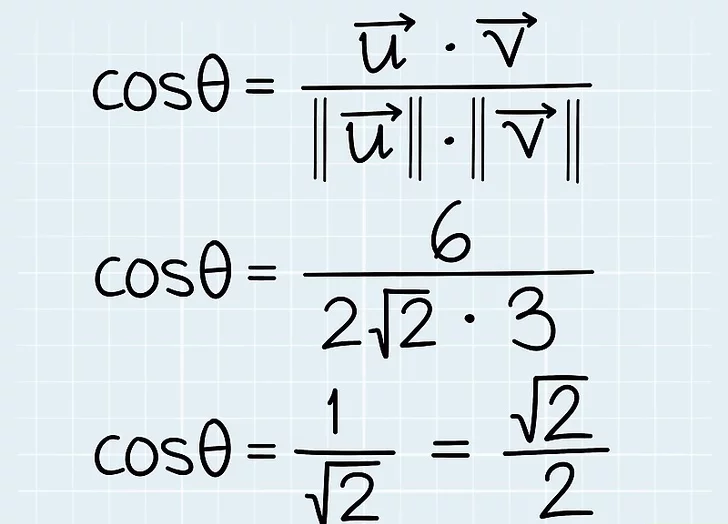
5. حاصل ضرب نقطه و قدر هر بردار را به فرمول وصل کنید. به یاد داشته باشید، فرمول این  است اکنون که هم حاصل ضرب نقطه و هم بزرگی هر بردار را می دانید، به سادگی آنها را در این فرمول وارد کنید.
است اکنون که هم حاصل ضرب نقطه و هم بزرگی هر بردار را می دانید، به سادگی آنها را در این فرمول وارد کنید.
حتما بخوانید: روش محاسبه محیط و مساحت ذوزنقه تصویری
یافتن کسینوس با حاصلضرب نقطه و بزرگی
.در مثال ما، برای بدست آوردن
برای بدست آوردن  ساده کنید.
ساده کنید.
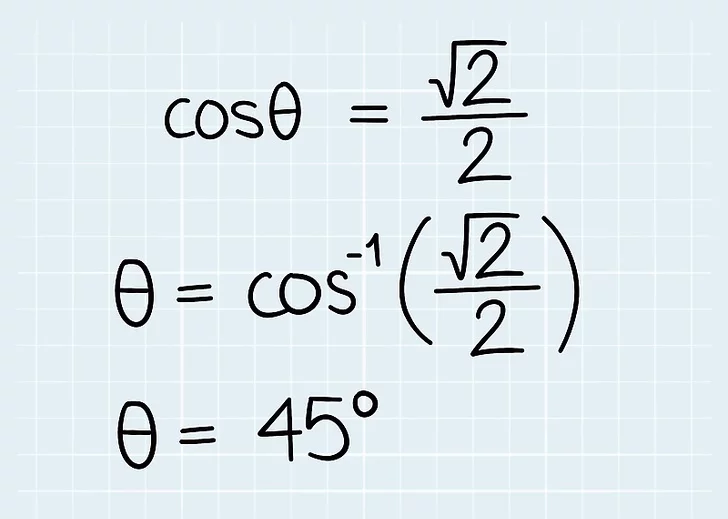
6. از یک ماشین حساب علمی برای یافتن زاویه بر اساس کسینوس استفاده کنید. در اکثر ماشینحسابها، از تابع arccos یا cos -1 در ماشین حساب خود برای پیدا کردن زاویه θ استفاده کنید. به سادگی "arccos" را وارد کنید و حاصل ضرب نقطه بر قدر بردارها را تقسیم کنید. برای برخی از نتایج، از دایره واحد برای تعیین زاویه استفاده کنید.
پیدا کردن یک زاویه با کسینوس
در مثال ما، θ = cos -1 (√2 / 2). "arccos(√2 / 2)" را در ماشین حساب خود وارد کنید تا θ = 45 درجه را بدست آورید. از طرف دیگر، زاویه θ را روی دایره واحد پیدا کنید که cosθ = √2/2 باشد.
روش 2: با استفاده از فرمول محصولات متقابل

1. از فرمول استفاده کنید. این فرمول از سینوس و حاصل ضرب بردارها برای یافتن زاویه بین آنها استفاده می کند. بر خلاف فرمول حاصلضرب نقطهای که به شما پاسخی اسکالر میدهد، فرمول ضربدری به صورت بردار به شما پاسخ میدهد. در این فرمول:
استفاده کنید. این فرمول از سینوس و حاصل ضرب بردارها برای یافتن زاویه بین آنها استفاده می کند. بر خلاف فرمول حاصلضرب نقطهای که به شما پاسخی اسکالر میدهد، فرمول ضربدری به صورت بردار به شما پاسخ میدهد. در این فرمول:
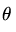 زاویه بین بردارها است.
زاویه بین بردارها است.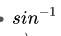 معکوس سینوس است.
معکوس سینوس است. حاصلضرب متقاطع بردار u و vاست.
حاصلضرب متقاطع بردار u و vاست.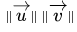 قدر مطلق بردار u و v است.
قدر مطلق بردار u و v است.
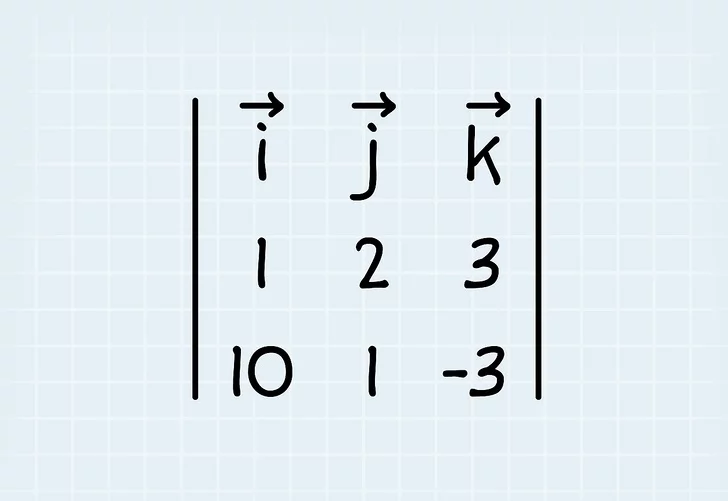
2. حاصل ضرب متقاطع را با استفاده از مختصات بردارها پیدا کنید. در اکثر مسائل ریاضی، مختصات ابعادی یا اجزای هر بردار را دارید که به صورت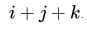 نوشته شده است . برای یافتن حاصل ضرب، ماتریسی با مختصات بردار اول در ردیف اول و مختصات بردار دوم در ردیف دوم ایجاد کنید. مقادیر i، j و k را برای هر بخش ماتریس محاسبه کنید.
نوشته شده است . برای یافتن حاصل ضرب، ماتریسی با مختصات بردار اول در ردیف اول و مختصات بردار دوم در ردیف دوم ایجاد کنید. مقادیر i، j و k را برای هر بخش ماتریس محاسبه کنید.
حتما بخوانید: حل مساحت مربع با مثال
- به عنوان مثال، زاویه بین 2 بردار را پیدا کنید که در آن 1i + 2j + 3k u است.
- یک ماتریس u : 1 2 3 در ردیف بالا و 10 1 -3 در ردیف پایین است.
- ماتریس i را حل کنید: i = (u j * v k ) - (v j * u k )
i = (6 - 3) = 3
- ماتریس j را حل کنید: j = (u i * v k ) - (v i * u k )
j = (-3 - 30) = -33
- حل ماتریس برای k: k = (u i * v j ) - (v i * u j )
k = (1 -20) = 21
- مختصات i - j + k را پیدا کنید: 3i - -33j + 21k = 3i + 33j + 21k یا <3, 33, 21>

3. قدر حاصل ضرب را محاسبه کنید. آخرین مرحله در یافتن حاصل ضرب بردارها، یافتن بزرگی مختصات آنهاست. به یاد داشته باشید، از قضیه فیثاغورث برای یافتن قدر بردار استفاده کنید.
- فقط مختصات i، k، j حاصل ضرب بردارها را وصل کنید تا قدر آنها را بدست آورید.
- محصول متقاطع از 3i + 33j + 21k u *vیا <3، 33، 21> است.از قضیه فیثاغورث برای یافتن قدر استفاده کنید: || uxv || = √(i 2 + j 2 + k 2 )
- 3i + 33j + 21k را به قضیه وصل کنید: √((3) 2 + (33) 2 + (21) 2 )
- حل: √9 + 1089 + 441 = 1539 √
- حاصلضرب متقاطع بردار
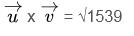
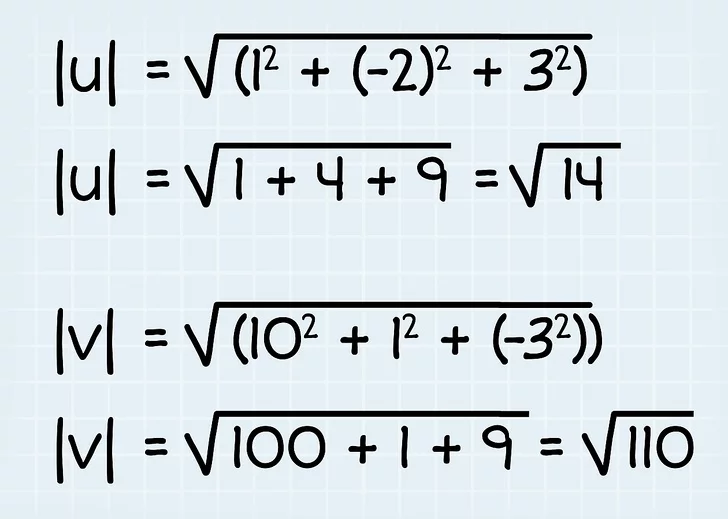
4. قدر هر بردار را بیابید. حال، قدر هر بردار را با استفاده از مختصات ابعادی آنها محاسبه کنید. فقط مختصات را مانند مرحله بالا به قضیه فیثاغورث وصل کنید.
- در مثال 1i+2j+3k u است و 10i + 1j - 3k v است.
- قدر : || u || = √i 2 + j 2 + k 2 = √((1) 2 + (-2) 2 + (3) 2 ) = √1 + 4 + 9 = √14 بیابید.
- قدر : || v || = √((10) 2 + (1) 2 + (-3) 2 ) = √100 + 1 + 9 = √110 بیابید
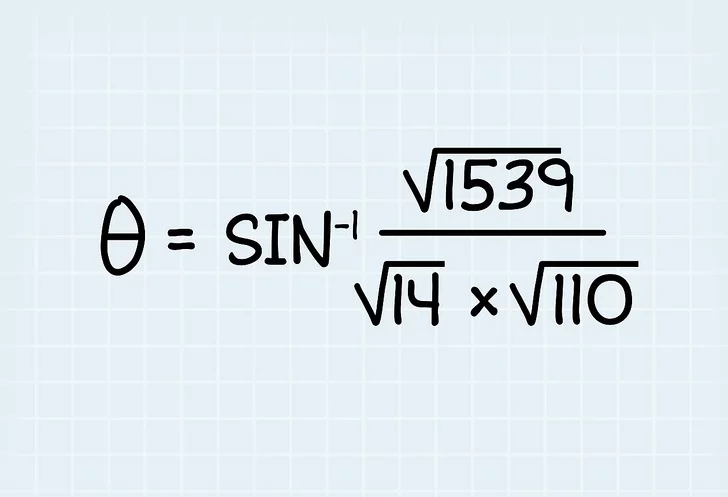
5. حاصل ضرب متقاطع و جذر بردارها را به فرمول اضافه کنید. اکنون که حاصل ضرب و جذر بردارها را دارید.
حتما بخوانید: دانلود 8 برنامه اندازه گیری، قد، مساحت برای گوشی
- به سادگی آنها را در فرمول
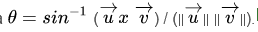 وارد کنید.
وارد کنید.
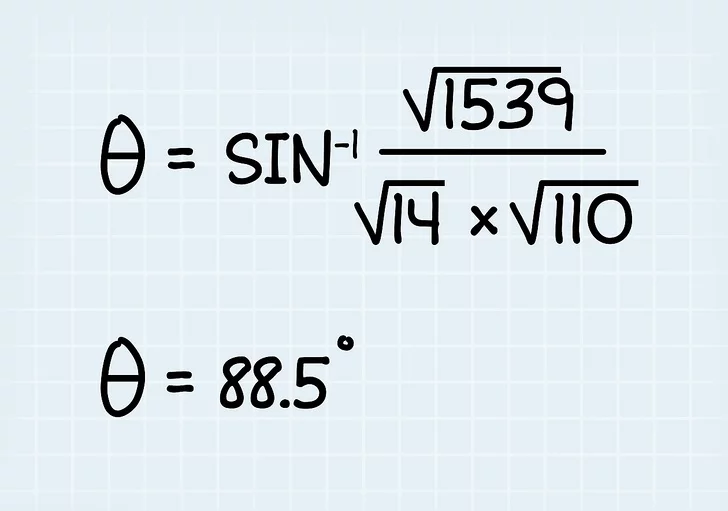
6. با استفاده از ماشین حساب زاویه را پیدا کنید. به سادگی سینوس معکوس حاصل ضرب و قدر را بگیرید تا زاویه بین بردارها را پیدا کنید. با استفاده از ماشین حساب خود، تابع arcsin یا sin -1 را پیدا کنید . سپس، حاصل ضرب و قدر را وارد کنید.
- در مثال ما، "arcsin(√1539 / √14 * √110) را در ماشین حساب خود وارد کنید تا θ = 88.5 درجه را بدست آورید.
روش 3. درک فرمول اسکالر
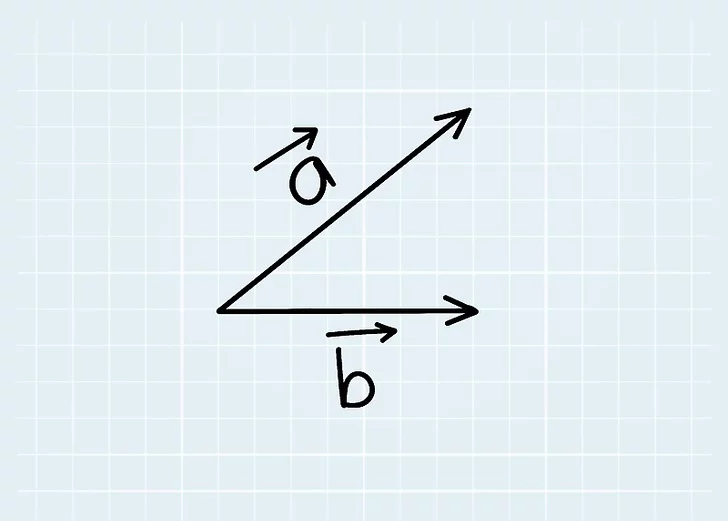
1. هدف فرمول زاویه را درک کنید
این فرمول از قوانین موجود استخراج نشده است. در عوض، به عنوان تعریفی از حاصل ضرب نقطه 2 بردار و زاویه بین آنها ایجاد شد. با این حال، این تصمیم خودسرانه نبود. با نگاهی به هندسه پایه، می بینید که چرا این فرمول به تعاریف بصری و مفیدی منجر می شود.مثالهای زیر از بردارهای دو بعدی استفاده میکنند، زیرا این بردارها بصریترین روشها برای استفاده هستند. بردارهایی با 3 جزء یا بیشتر از همین فرمول استفاده می کنند.
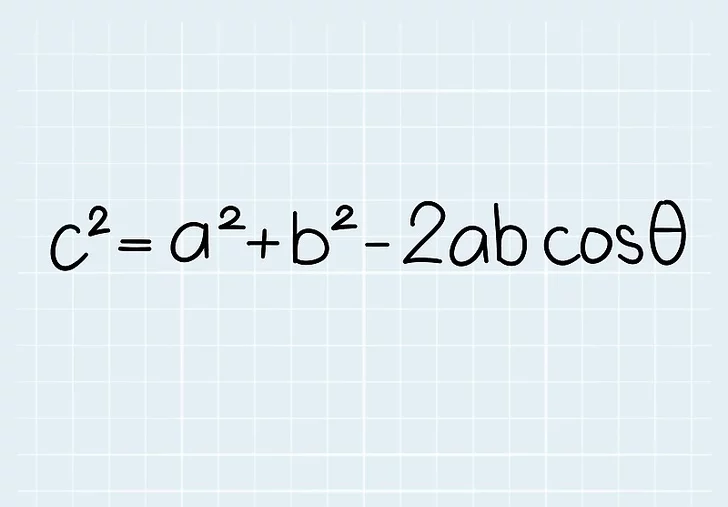
2. قانون کسینوس استفاده شده در فرمول را مرور کنید
یک مثلث معمولی با زاویه θ بین ضلع a و b و ضلع مقابل c در نظر بگیرید. قانون کسینوس می گوید که c 2 = a 2 + b 2 -2ab cos (θ). این به راحتی از هندسه پایه به دست می آید.
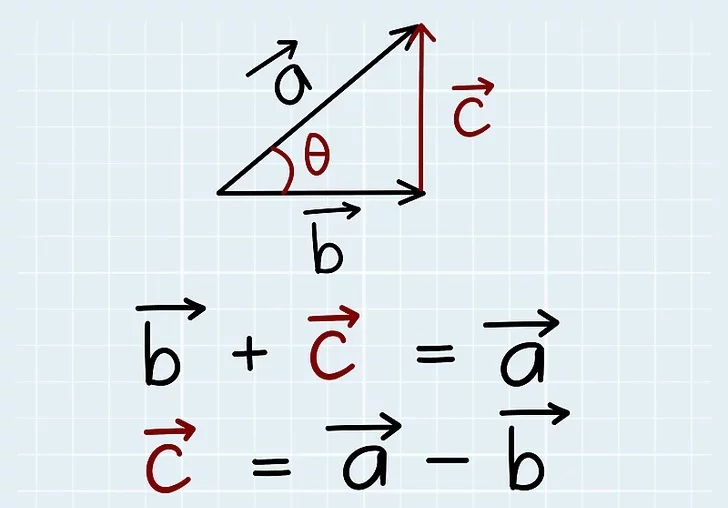
3. 2 بردار را به هم وصل کنید تا یک مثلث تشکیل دهید
یک جفت مولفه دوبعدی را روی کاغذ ترسیم کنید، با زاویه θ بین آنها. بردار سومی بین آنها رسم کنید تا مثلث بسازید.

4. قانون کسینوس ها را برای مثلث بنویسید
طول اضلاع "مثلث برداری" را در مثال ما در قانون کسینوس وارد کنید

5. قانون کسینوس ها را با استفاده از حاصل ضرب نقطه ای بردار a و b بنویسید
به یاد داشته باشید، حاصل ضرب نقطه، بزرگنمایی 1 بردار است که بر روی دیگری پیش بینی می شود. حاصلضرب نقطه بردار با خودش نیازی به نمایش ندارد، زیرا هیچ تفاوتی در جهت وجود ندارد. این به این معنی است که 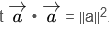 از این واقعیت برای بازنویسی معادله استفاده کنید
از این واقعیت برای بازنویسی معادله استفاده کنید
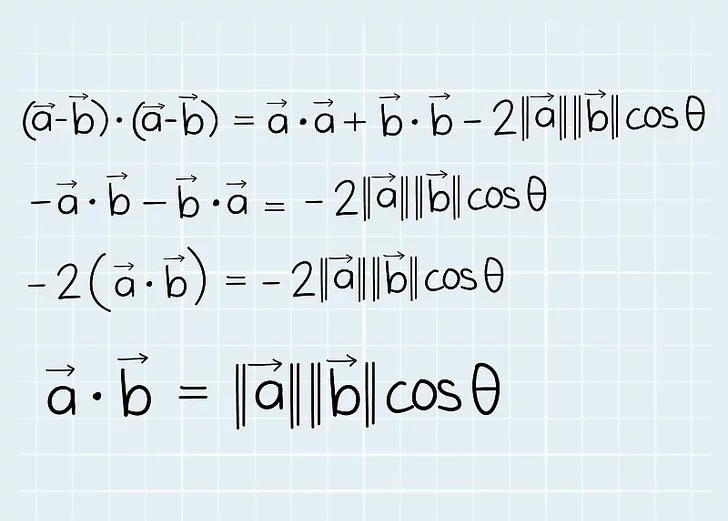
6. محصول اسکالر را در فرمول زاویه بازنویسی کنید. سمت چپ فرمول را باز کنید، سپس آن را ساده کنید تا به فرمول مورد استفاده برای یافتن زاویه برسید.

سوالات متداول
چگونه زاویه بین دو بردار را پیدا کنم؟ برای مثال، بردار A = 4i + 2j - 2k و بردار B = 3i +2j + 3k؟
از فرمول θ = cos^-1 (a * b) / ||aاستفاده کنید. برای بدست آوردن حاصل ضرب نقطه، Ai را در Bi، Aj را در Bj و Ak را در Bk ضرب کنید سپس مقادیر را با هم جمع کنید. برای پیدا کردن قدر A و B، از قضیه فیثاغورث (√(i^2 + j^2 + k^2) استفاده کنید. سپس، از ماشین حساب خود استفاده کنید تا کسینوس معکوس حاصل ضرب نقطهای را جذر بگیرید و به دست آورید.
اگر فرمول کسینوس به من 0 بدهد، به این معنی است که بردار عمود هستند. اما چگونه بفهمم 90 درجه است یا -90 درجه؟
زاویه بین 2 بردار همیشه بین 0 تا 180 درجه است، بنابراین زاویه 90 درجه است.
در مثال بالا cosθ 1/√2 بود. اما در اینجا cosθ می تواند 45 درجه یا 315 درجه باشد. چرا جواب 315 نیست؟
وقتی زاویه بین 2 بردار را پیدا کنید، زاویه همیشه بین 0 تا 180 درجه خواهد بود.
سخن آخر
در این مطلب با روش ها پیدا کردن زاویه بین 2 بردار آشنا شدید. امیدواریم که از این مطلب استفاده و لذت برده باشید.


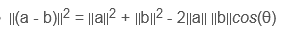
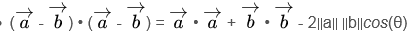
دیدگاه ها