در این درس از ریاضی هشتم، به دانشآموزان یاد داده میشود که چگونه کسرها را ساده کرده و عبارتهای جبری را به ضرب تبدیل کنند. تمرینها شامل شناسایی عامل مشترک و تجزیه جملات جبری است. در این مقاله از سلام دنیا به حل فعالیت صفحه 60 ریاضی هشتم با توضیح مرحله به مرحله و پاسخ تشریحی پرداختهایم.
حل فعالیت صفحه 60 ریاضی هشتم با جواب
سوال 1 صفحه 60 ریاضی پایه هشتم با توضیح
1. در دوره دبستان یاد گرفتید که با تبدیل صورت و مخرج کسر به ضرب عددها، میتوان کسر را ساده کرد. کسرهای زیر را مانند نمونه ساده کنید.
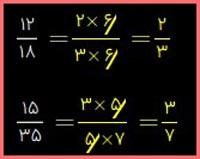
////////////////////////////////////////////////////////////////
حتما بخوانید: حل تمرین صفحه 61 ریاضی هشتم
/////////////////////////////////////////////////////////
سوال 2 صفحه 60 ریاضی پایه هشتم با توضیح
2. بعضی از عبارتهای جبری را نیز میتوان به صورت ضرب دو یا چند عبارت نوشت:
- خاصیت توزیع پذیری a(b+c)=ab+ac
- (تبدیل به ضرب) تجزیه کردن ab+ac=a(b+c)
با توجه به تساوی بالا، عبارتها را به ضرب تبدیل کنید.
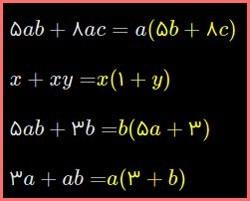
////////////////////////////////////////////////////////////////
سوال 3 صفحه 60 ریاضی پایه هشتم با توضیح
3. برای تجزیه یک عبارت جبری، عامل یا بخش مشترک دو یا چند جمله را پیدا میکنیم و بیرون پرانتز مینویسیم. برای تشخیص قسمت مشترک، میتوان عبارتها را به صورت ضرب نوشت:
- 6a2b3+9a3b2=2×3×a×a×b×b×b×+3×3×a×a×a×b×b
- 2×3×a2×b2×b+3×3×a2×b2×a
با توجه به تساوی بالا، عامل مشترک دو جملهٔ عبارت جبری چیست؟
- 3a2b2
با ضرب کردن چه عبارتی در جملهٔ مشترک، جملهٔ اول عبارت ساخته میشود؟
- 2b
با ضرب کردن چه عبارتی در جملهٔ مشترک، جملهٔ دوم عبارت ساخته میشود؟
- 3a
حالا این تساوی را کامل کنید.
- 6a2b3+9a3b2=3a2b2(2b+3a)
////////////////////////////////////////////////////////////////
ویدئو آموزش و حل صفحه 60 ریاضی هشتم
ویدئو آموزش و حل صفحه 60 ریاضی هشتم
سخن آخر
تمرینهای این صفحه مهارت دانشآموزان را در کار با کسرها و جملات جبری تقویت میکند و کمک میکند تا روابط بین اعداد و عوامل مشترک را بهتر درک کرده و مسائل پیچیدهتر را گام به گام حل کنند.
مطالب مرتبط:
جدول ارزش مکانی ریاضی کلاس دوم


دیدگاه ها