در این بخش از ریاضی هشتم، مفهوم توان عددها و عبارتهای جبری بررسی میشود. یاد میگیریم توان یعنی ضرب تکراری یک عدد در خودش، نه جمع آن، و با خاصیتهای ضرب و جابهجایی در عبارات تواندار آشنا میشویم. در این مقاله از سلام دنیا به حل گامبهگام فعالیت و کار در کلاس صفحه 62 ریاضی پایه هشتم با توضیح کامل و پاسخ تشریحی پرداختهایم.
حل فعالیت صفحه 62 ریاضی هشتم با جواب
سوال 1 صفحه 62 ریاضی پایه هشتم با توضیح
1. تفاوت x^2 و 2x چیست؟
- x^2= x × x
- 2x = x + x
/////////////////////////////////////////////////////////
حتما بخوانید: حل تمرین صفحه 63 ریاضی هشتم
/////////////////////////////////////////////////////////
سوال 2 صفحه 62 ریاضی پایه هشتم با توضیح
2. مانند نمونه، طرف دیگر تساویها را بنویسید.
- 3 × 3 = 2^3
- 5. × 5. = 2^(5.)
- a^2 = a × a
- ☑️ × ☑️ = 2☑️
- ꕔ2 = ꕔ × ꕔ
- (a+b)×(a+b) = به توان 2 (a+b)
/////////////////////////////////////////////////////////
سوال 3 صفحه 62 ریاضی پایه هشتم با توضیح
3. جدول زیر را برای مقدارهای مختلف a و b کامل کنید.
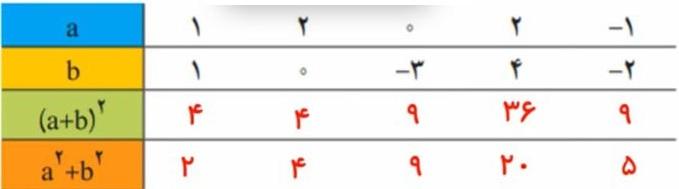
از مقایسه دو ردیف آخر، چه نتیجهای میگیرید؟
- نتیجه می گیریم 2^(a+b)≠a^2+b^2
/////////////////////////////////////////////////////////
سوال 4 صفحه 62 ریاضی پایه هشتم با توضیح
4. مانند نمونه، عبارتها را ساده کنید.

/////////////////////////////////////////////////////////
حل کار در کلاس صفحه 62 ریاضی هشتم با جواب
سوال 1 صفحه 62 ریاضی پایه هشتم با توضیح
1. مانند نمونه، تساویها را کامل کنید.
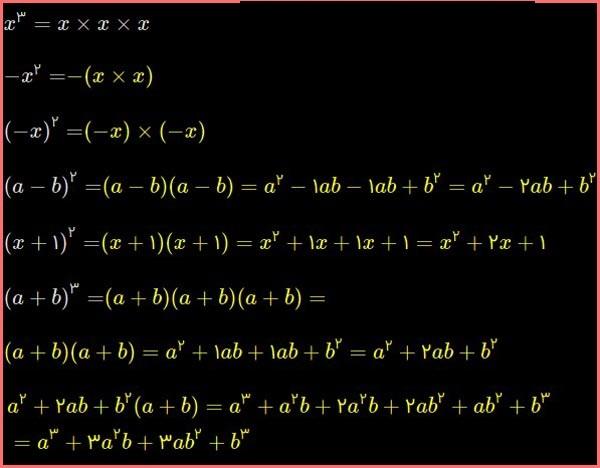
/////////////////////////////////////////////////////////
حتما بخوانید: حل تمرین صفحه 64 ریاضی هشتم
/////////////////////////////////////////////////////////
سوال 2 صفحه 62 ریاضی پایه هشتم با توضیح
2. چرا ba=ab است؟ (از کدام خاصیت ضرب استفاده میشود؟)
- خاصیت جابهجایی
/////////////////////////////////////////////////////////
سوال 3 صفحه 62 ریاضی پایه هشتم با توضیح
3. عبارت زیر را ساده کنید.
- −(a+b)2=
- −(a+b)(a+b)=−(a^2+1ab+1ab+b^2)
- =−(a^2+2ab+b^2)=−a^2−2ab−b^2
آیا منفی به توان 2 میرسد؟ چرا؟
- خیر . زیرا بیرون پرانتز هست.
/////////////////////////////////////////////////////////
ویدئو آموزش و حل صفحه 62 ریاضی هشتم
ویدئو آموزش و حل صفحه 62 ریاضی هشتم
سخن آخر
در این درس یاد گرفتیم که توان یعنی ضرب تکراری، نه جمع. همچنین دیدیم هنگام به توان رساندن مجموع یا تفاضل، باید از فرمولهای اتحاد مربع مجموع و مربع تفاضل استفاده کنیم. درک درست این مفاهیم، پایهی مهمی برای حل معادلات و اتحادهای جبری در پایههای بعدی است.
مطالب مرتبط:
جدول ارزش مکانی ریاضی کلاس دوم


دیدگاه ها